Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.
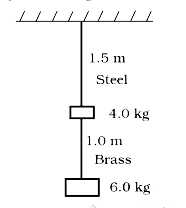
L=1.5m, diameter = 0.25cm,
Radius =r=0.125×10−2m,A=πr2
Force =6+4=10kg wt =10×0.8N,
Y=2.0×1011Pa
Y=FLAl,l=FLYA
l=98×1.52×1011×3.14×(0.215×10−2)2
=1.5×10−4 m
Brass. L=1.0m
r=0.125×10−2m,A=πr2
F=6×9.8N
Y=0.91×1011Pa
l=FLYA
=6×9.8×10.91×1011×3.14×(0.125×10−2)2
=1.317×10−4m
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2 (SOLVED EXAMPLES)
22 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (SOLVED EXAMPLES)
31 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.
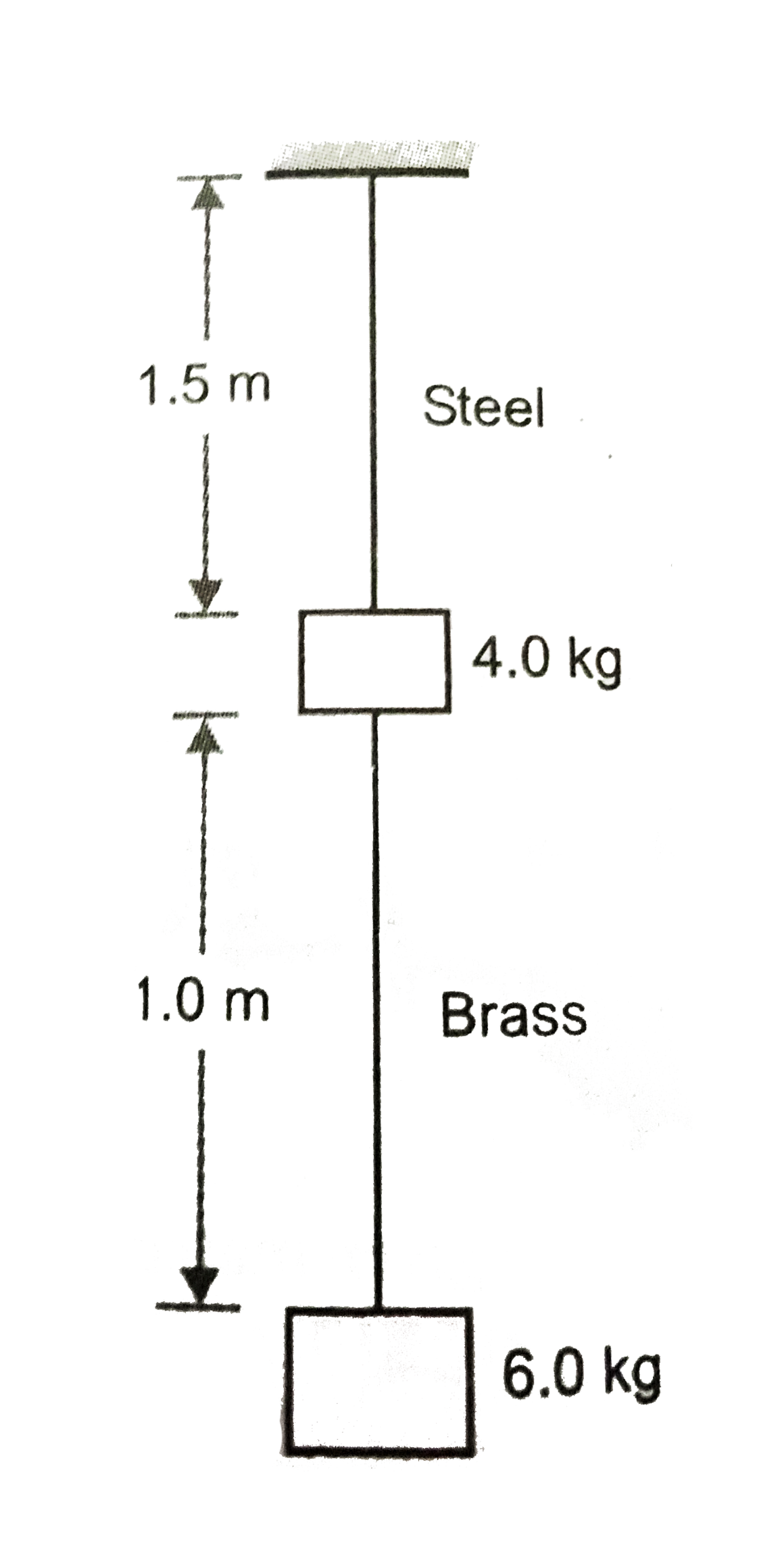
View SolutionTwo wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?

View Solution
Knowledge Check
A 10 m long steel wire has mass 5 g. If the wire is under a tension of 80 N, the speed of transverse waves on the wire is
A100ms−1B200ms−1C400ms−1D500ms−1
The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionTwo wires of equal cross section but one made of steel and the other of copper, are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. Find the ratio of the lengths of the two wires. Young modulus of steel =2.0×1011Nm−2 and that of copper =1.1×1011Nm−2
View SolutionA steel wire and copper wire of the same diameter and of length 1m and 2m respectively are connected end to end and a force is applied. The increase in length of the combination is 0.01m.Calculate the elongation produced in the individual wires. Given that Y of copper is 12×1010Nm2 and that of steel is 20×1010Nm−2.
View SolutionIn figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinal strains developed in the two wires.

View SolutionA 1m long wire of diameter 0.31mm has a resistance of 4.2Ω. If it is replaced by another wire of same material of length 1.5m and diameter 0.155mm, then the resistance of wire is
View SolutionAn iron wire AB of length 3m at 0∘C is stretched between the oppsote walls of a brass casing at 0∘C. The diameter of the wire is 0.6mm. What extra tension will be set up in the wire when the temperature of the system is rasied to 40∘C?
Given abrass=18×10−6/k
airon=12×10−6/K
Yiron=21×1010N/m2
View SolutionA piece of steel wire (diameter = 0.075 cm and length 5.08 m) elongates by 0.7 cm due to a load of 12.7 kg. Find Young.s modulus of steel.
View Solution
