Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
2p0(r3−r31−r32)4(r21+r22−r2)
p0(r3−r31−r32)4(r21+r22−r2)
p0(r3+r21+r32)4(r21+r22+r2)
None of these
The correct Answer is:B
As mass of the air is conserved,
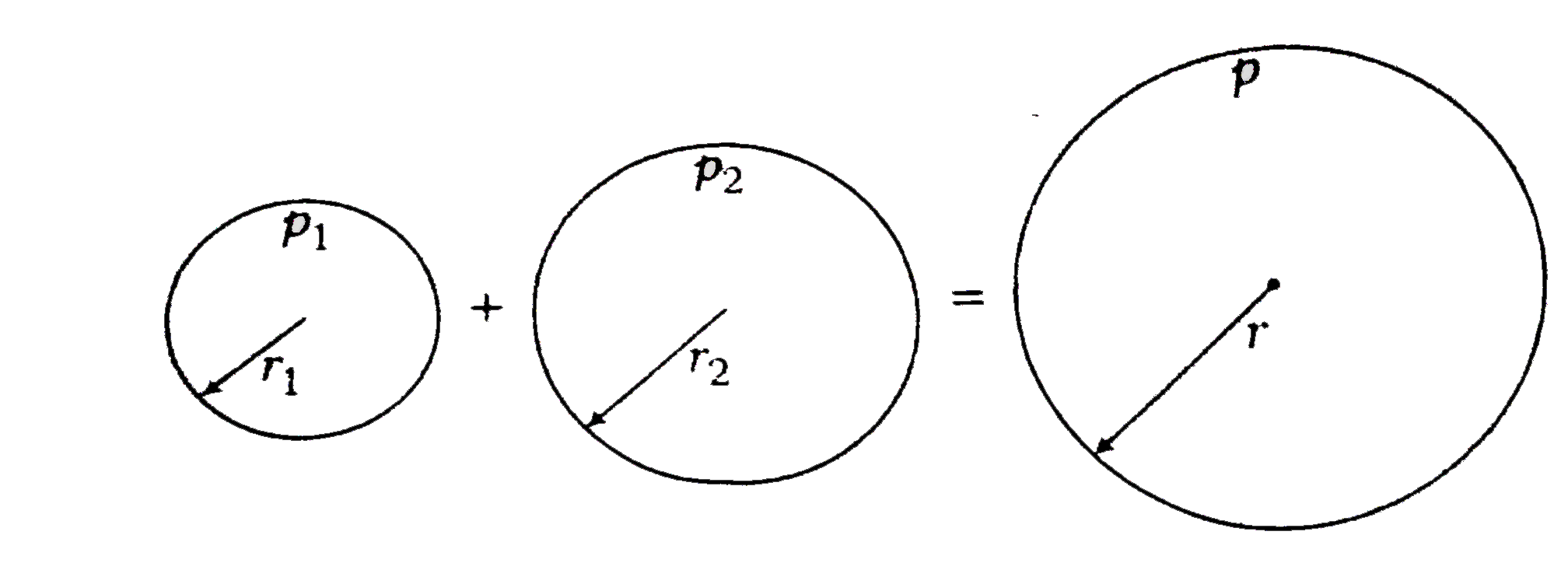
∴ n1+n2=n (aspV=nRT)
∴p1V1RT1+p2V2RT2=pVRT
As temperature is constant,
T1=T2=T
∴p1V1+p2V2=pV
∴(p0+4Sr1)(43πr31)+(p0+4Sr2)(43πr32)=(p0+4Sr)(43πr3)
Solving, this we get
S=p0(r3−r31−r32)4(r1r2+r22−r2)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View Solution
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2The radii of two soap bubbles are r1andr2(r2<r1). They meet to produce a double bubble. The radius of their common interface is
Ar1r2r1+r2Br1+r22Cr1r2r1−r2Dr2−r1
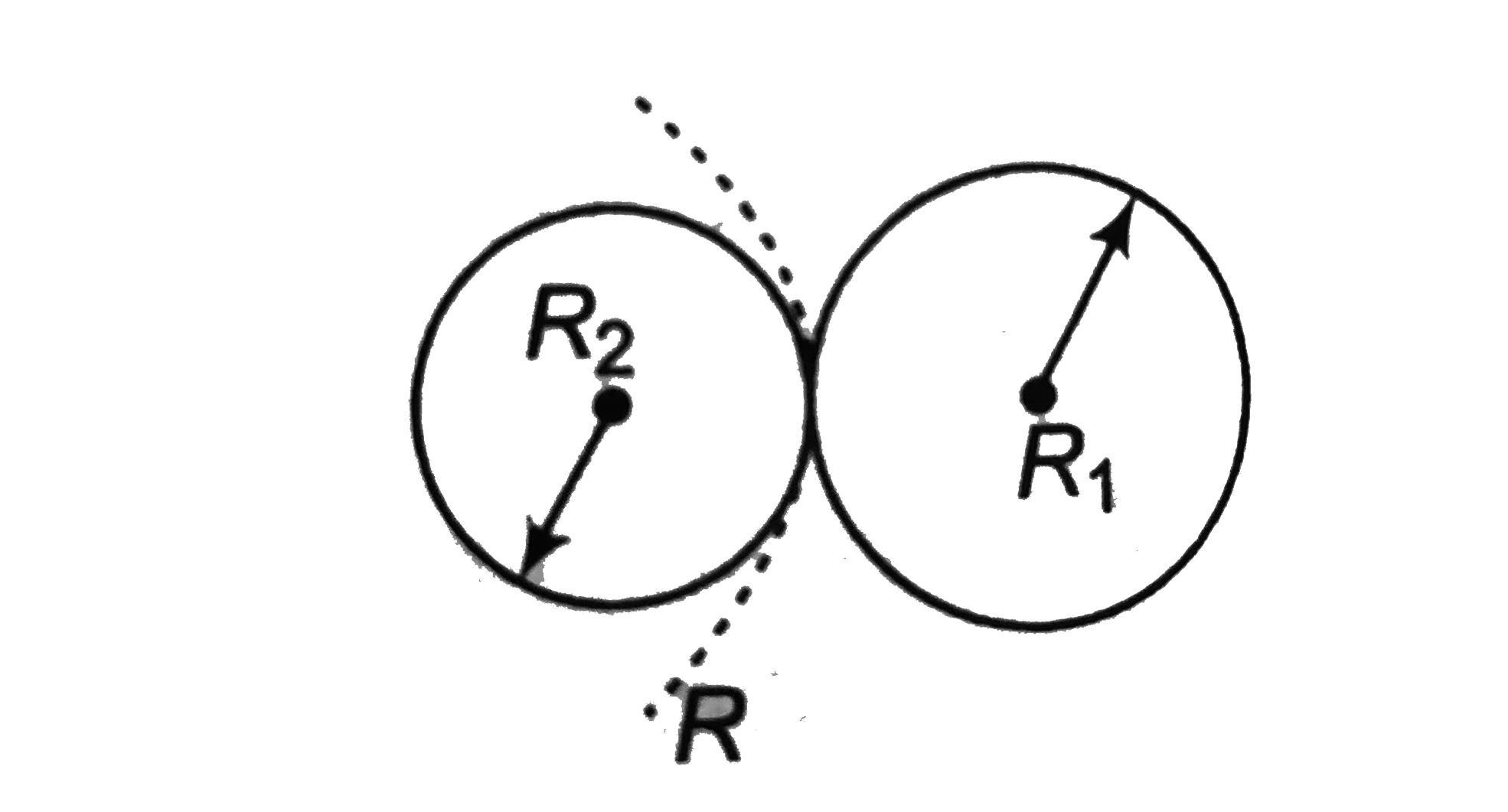
Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .
.
View SolutionAir is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View SolutionA soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
View SolutionTwo soap bubbles in vacuum of radius 3cm and4cm coalesce to form a single bubble, in same temperature. What will be the radius of the new bubble
View Solution
