
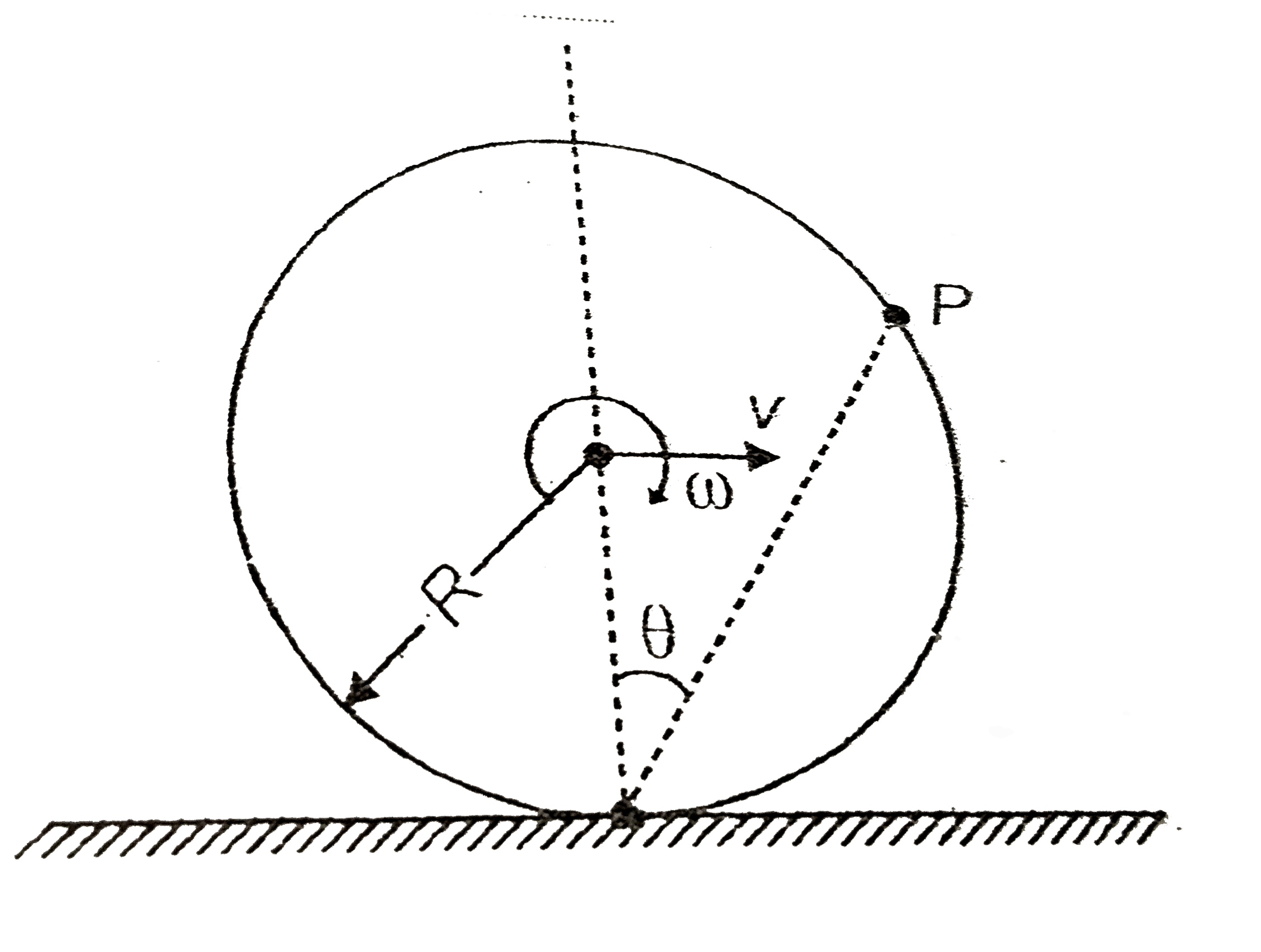
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.
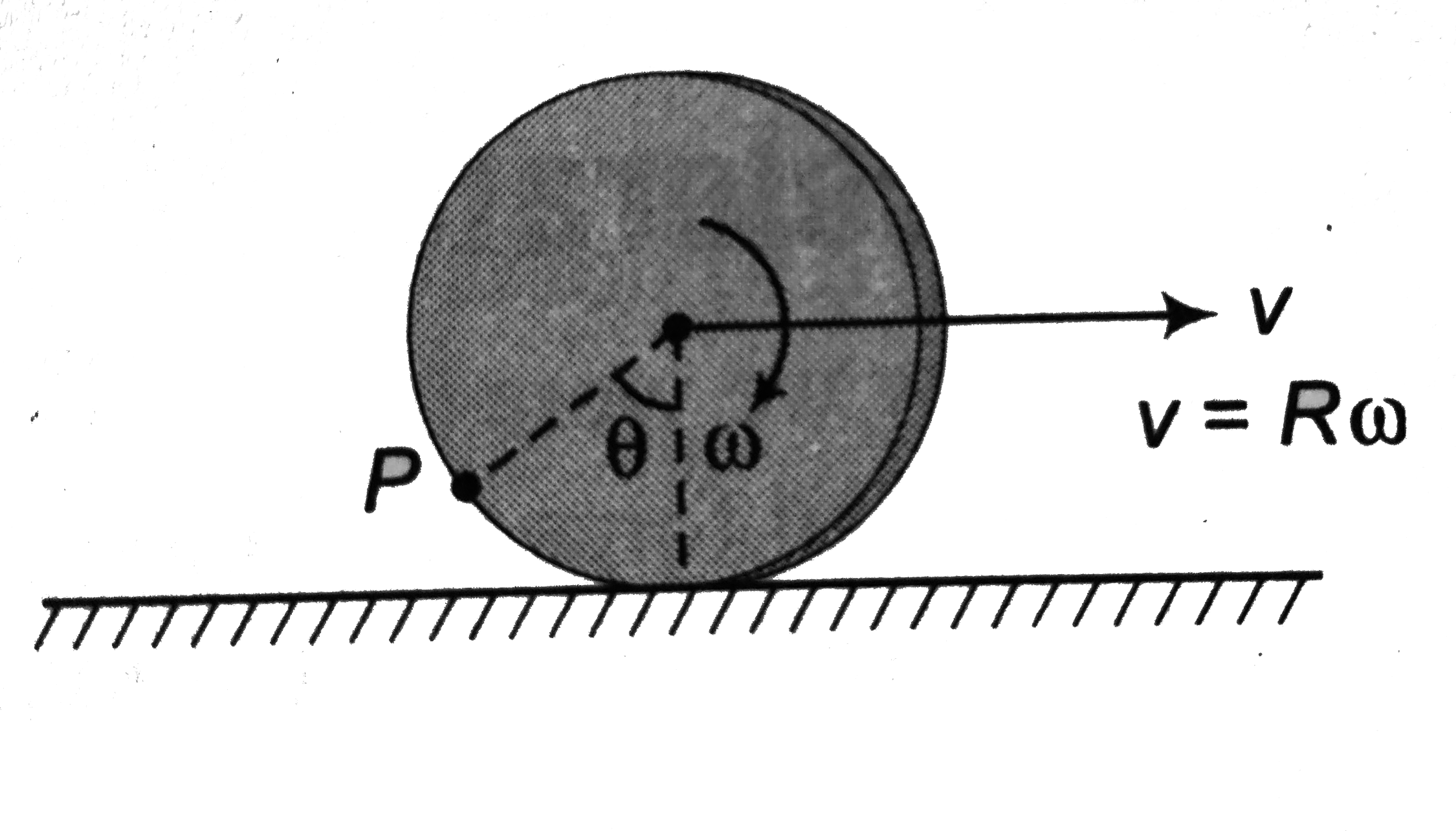
In pure rolling, combined rotation and translation motion may be assumed to be a pure rotational motion about an axis passing through bottommost point (with same ω) or instantaneous axis of rotation
|VP|=(OP)ω here OP=2Rsin(θ2)
therfore|VP|=(2Rsin(θ2)ω=2Rωsin(θ2)=2vsin(θ2)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Solved Examples
Explore 25 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions

A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View SolutionA ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is (6ˆi−8ˆj)m/s2. Find the angular acceleration of the ring & the abgular velocity at that instant. Radius of the ring is 2m.

View Solution
Knowledge Check
velocity time graph of a particle is shown in figure. Find displacement of the particle.
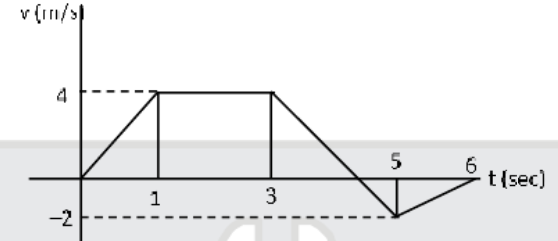 A7B11C5D15
A7B11C5D15A particle is going in a spiral path as shown in figure with constant speed.
 .AThe velocity of the particle is constant.BThe acceleration of the particle is constantCThe magnitude of acceleration is constant.DThe magnitude of accelertioin is decreasing continously
.AThe velocity of the particle is constant.BThe acceleration of the particle is constantCThe magnitude of acceleration is constant.DThe magnitude of accelertioin is decreasing continouslyA disc is rolling on a rough horizontal surface. The instantaneous speed of the point of contact during perfect rolling is zero with respect to ground.
The force of friction can help in achieving pure rolling condition.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
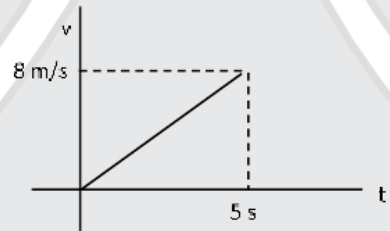
Speed time graph of a particle shown in figure. Find distance travelled by particle in 5second.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
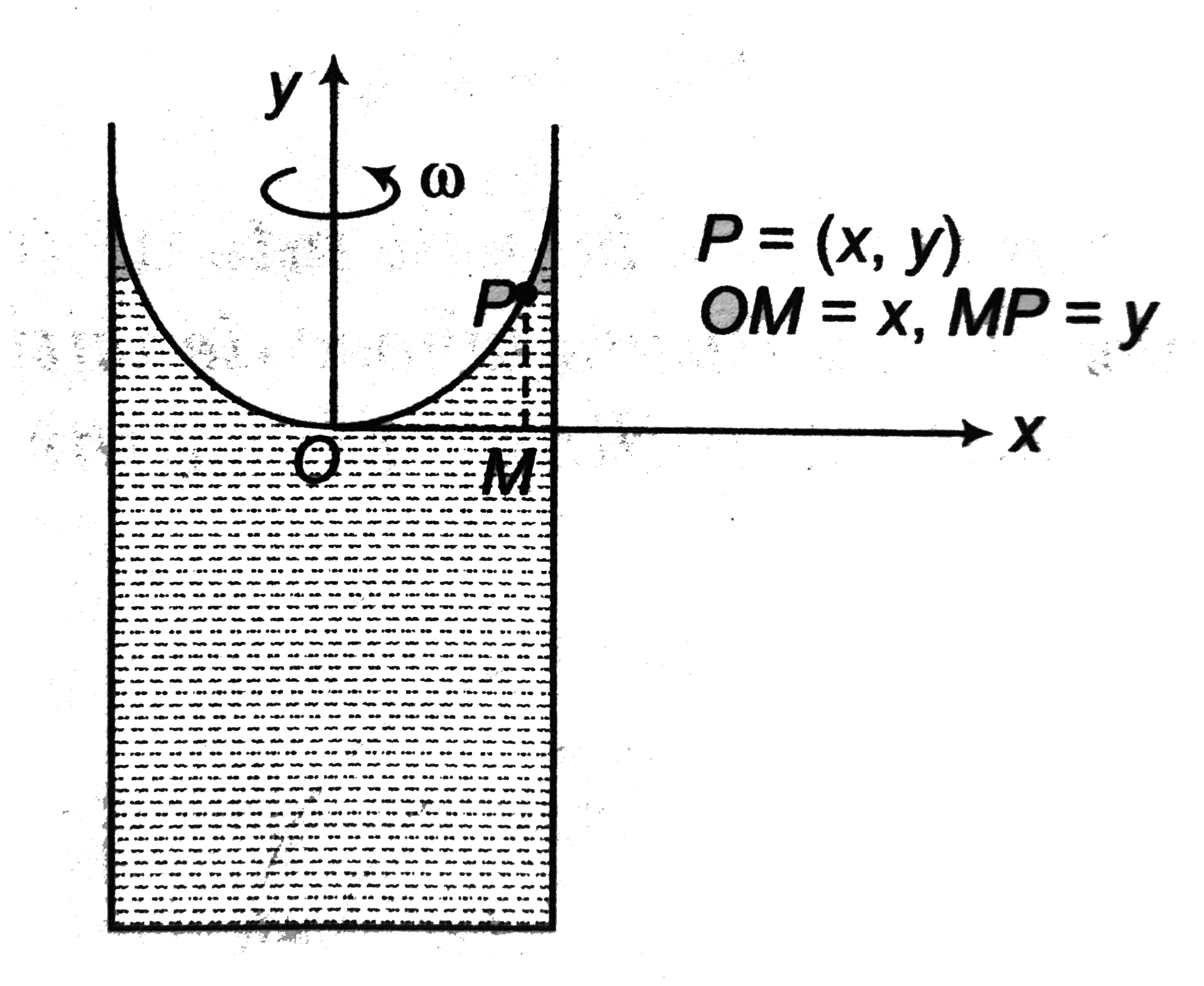 .
.
View SolutionThe velocity of a point P on the surface of a pure rolling disc as shown in figure, can be calculated as given below.
View SolutionAssertion : Speed of any point on rigid body executing rolling motion can be calculated by expression v=rω, where r is distance of point from intantaneous centre of rotation
Reason : Rolling motion of rigid body can be considered as a pure rotation about instantaneous centre of rotation.
View Solution
