Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R → Radius of the Earth)Solution in Tamil


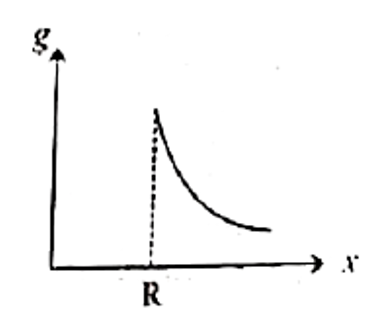
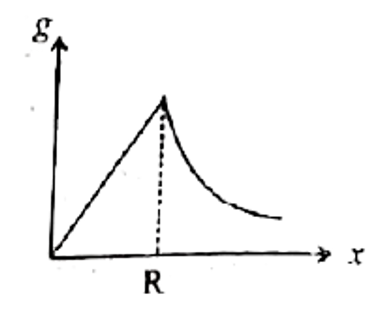
The correct Answer is:D
Acceleration due to gravity.
g=⎧⎨⎩GMR3x x<RGMx2 x≥R
Topper's Solved these Questions
- GRAVITATIONBOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (VERY SHORT ANSWER QUESTION)
43 Videos
- GRAVITATIONBOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (SHORT ANSWER QUESTIONS)
28 Videos
- GRAVITATIONBOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEXTBOOK QUESTION & ANSWERS (NUMERICAL PROBLEMS)
30 Videos
- KINEMATICS BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (V. Numerical problems).
166 Videos
Similar Questions
Distinguish between the terms gravitation and gravity.
View SolutionDefine 'G'. What are the units and dimensions of 'G' ?
View SolutionAn unknown planet orbits the Sun with distance twice the semi major axis distance of the Earth's orbit. If the Earth's time period is T2, what is the time period of this unknown planet.
View SolutionA crow is sitting on a branch of tree whose co-ordinates are (1,2,3) . A hunter is standing on the ground . Represent the position of the crow with respect to the hunter .
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r<R) from the centre of the earth is proportional to
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r>R) from the centre of the earth is proportional to
View SolutionAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionThe satellite is moving round the earth (radius of earth = R) at a distance r from the centre of the earth. If g is the acceleration due to gravity on the surface of the earth. The acceleration of the satellite will be
View SolutionThe variation of acceleration due to gravity g with distance d from centre of the earth is best represented by (R = earth's radius )
View SolutionVariation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
View SolutionThe acceleration due to gravity at a distance x from the centre of earth is 8ms^(-2) . The earth shrinks in radius by 5% but its mass remains constant. The acceleration due to gravity at a disatance 'x' from the centre of earth now is:
View SolutionVariation of acceleration due to gravity (g) with distance x from the centre of the earth is best represented by (R → Radius of the earth)
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r gt R) from the centre of the earth is proportional to
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View Solution
