Vectors →Aand→B are mutually perpendicular . Component of →A+→B in the direction of →A−→B will be:
A2+B2√A2−B2
√A2−B2
A+BA−B
A2−B2√A2+B2
The correct Answer is:D
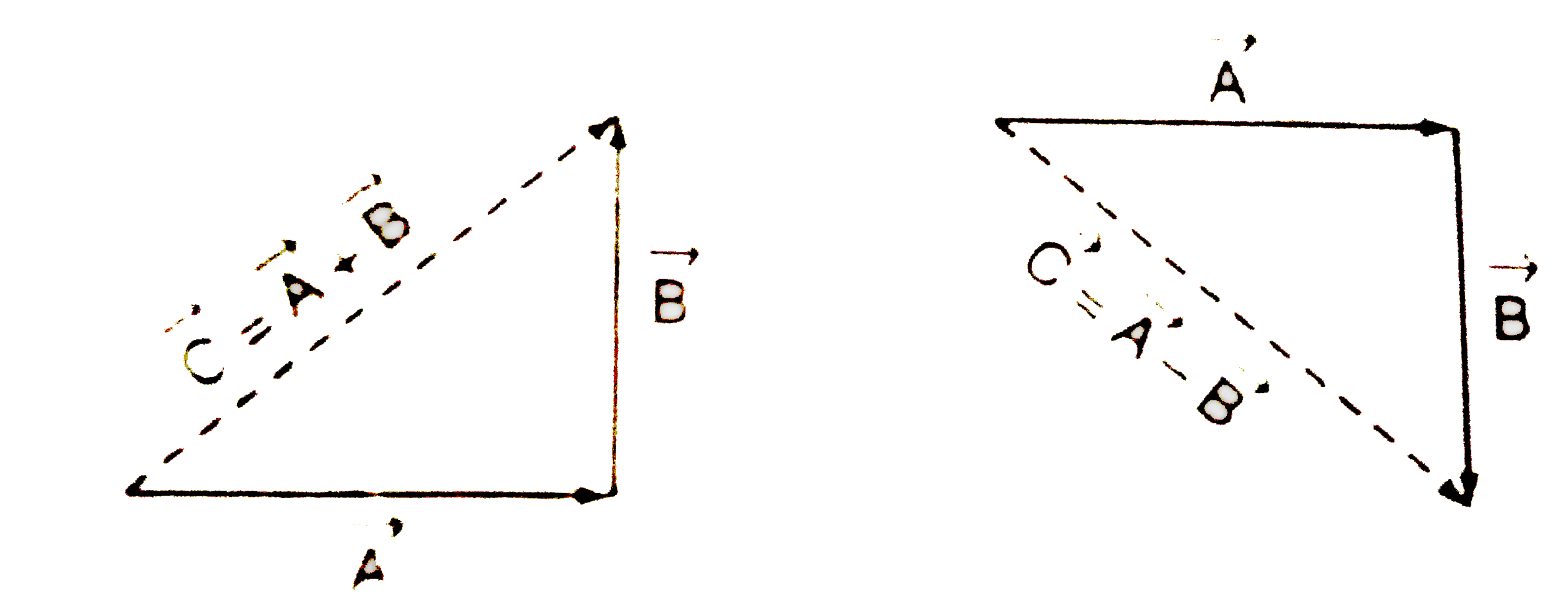
Component = (→A+→B).(→A−→B)√A2+B2
Topper's Solved these Questions
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - MORE THAN ONE CHOICE IS CORRECT
15 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - ASSERTION- REASON
1 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - PROBLEMS FOR PARCTICE
23 Videos
- UNITS AND DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression
6 Videos
Similar Questions
The resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View SolutionIf →a,→band→c are three mutually perpendicular unit vectors and →d is a unit vector which makes equal angal with →a,→band→c, then find the value of ∣∣→a+→b+→c+→d∣∣2.
View Solution
Knowledge Check
If the vectors →a and →b are mutually perpendicular, then →a×{→a×{→a×{→a×→b}} is equal to:
A|→a|2→bB|→a|3→bC|→a|4→bDNone of theseVectors 3→a−5→band2→a+→b are mutually perpendicular. If →a+4→band→b−→a are also mutually perpendicular, then the cosine of the angle between →anad→b is
A195√43B193√43C19√45D196√43If →a and →b are mutually perpendicular unit vectors, →ris a vector satisfying →r.→a=0,→r.→b=1 and (→r→a→b)=1, then →r is:
A→a+(→a×→b)B→b+(→a×→b)C→a+(→a×→b)D→a−→b+(→a×→b)
If →a,→band→c are three mutually perpendicular unit vectors and →d is a unit vector which makes equal angal with →a,→band→c, then find the value of ∣∣→a+→b+→c+→d∣∣2.
View SolutionIf →a,→b,→c are mutually perpendicular vectors of equal magnitude show that →a+→b+→c is equally inclined to →a,→band→c
View SolutionFor vectors →A and →B, (→A+→B).(→A×→B) will be :
View SolutionVector →a is prepedicular to →b, componets of →a−→b along →a+→b will be :
View SolutionTwo vectors →A and →B are such that →A+→B=→A−→B. Then
View Solution
