For a particle in uniform circular motion , the acceleration $\to a$ at a point $p (R, θ)$ on the circle of radiu $R$ is ( Here $θ$ is measured from the $x - a ξ s$ )

A

$- \frac{v^{2}}{R} sin θ ˆ i + \frac{v^{2}}{R} cos θ ˆ j$

B

$- \frac{v^{2}}{R} cos θ ˆ i + \frac{v^{2}}{R} sin θ ˆ j$

C

$- \frac{v^{2}}{R} cos θ ˆ i + \frac{v^{2}}{R} sin θ ˆ j$

D

$- \frac{v^{2}}{R} ˆ i + \frac{v^{2}}{R} ˆ j$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

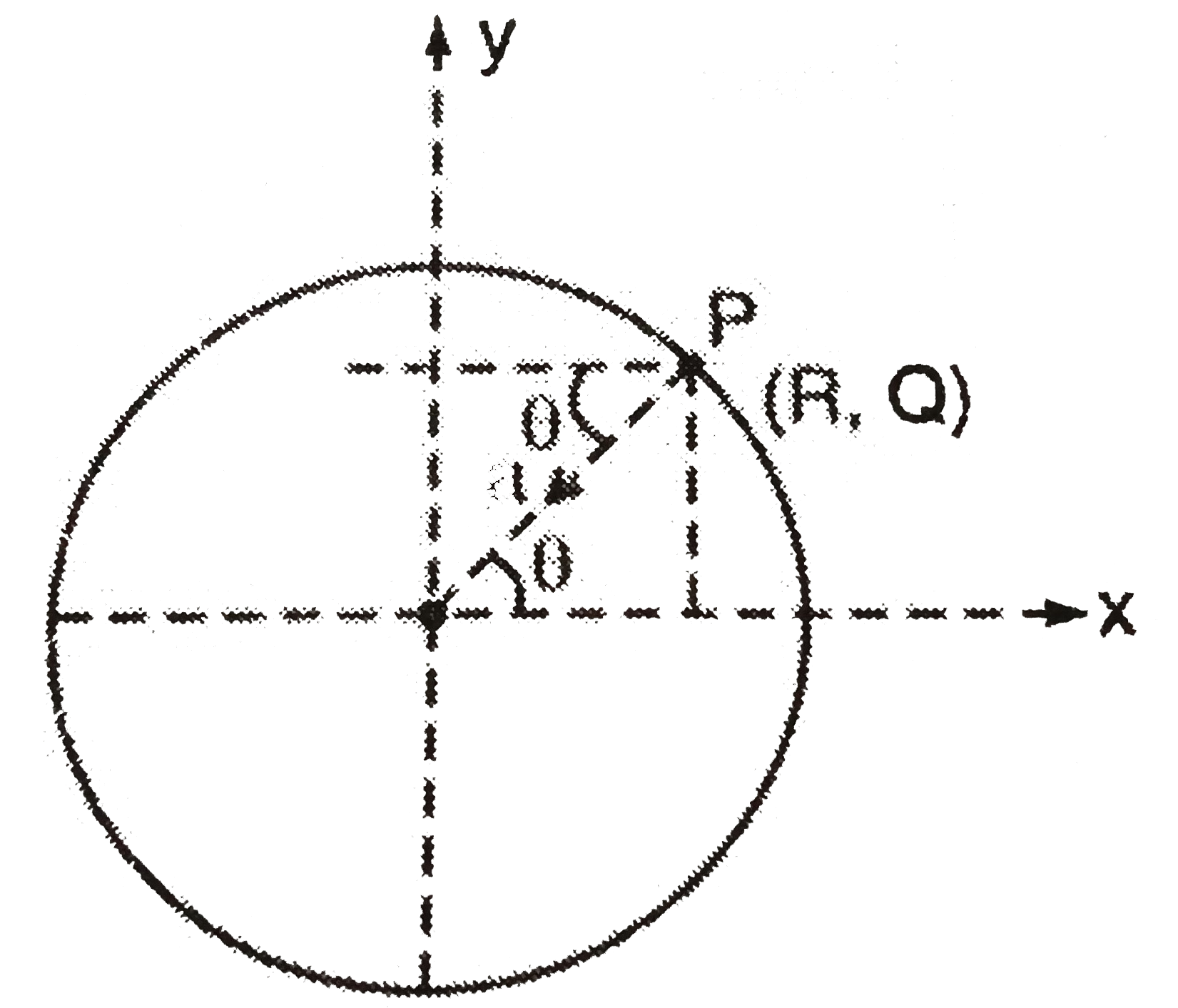
$\to a = a_{x} ˆ i - a_{y} ˆ j$
$\to a = \frac{v^{2}}{R} cos θ ˆ i - \frac{v^{2}}{R} sin θ ˆ j$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For a particle in uniform circular motion the acceleration $\to a$ at a point $P (R, θ)$ on the circle of radius R is : ( here $θ$ is measured from the x- axis )

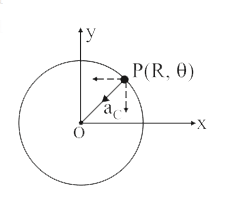A $- \frac{v^{2}}{R} cos θ ˆ i + \frac{v^{2}}{R} sin θ ˆ j$
B $- \frac{v^{2}}{R} sin θ ˆ i + \frac{v^{2}}{R} cos θ ˆ j$
C $- \frac{v^{2}}{R} cos θ h a i - \frac{v^{2}}{R} sin θ ˆ j$
D $\frac{v^{2}}{R} ˆ i + \frac{v^{2}}{R} ˆ j$
Question 2 - Select One
For a particle performing a uniform circular motion the acceleration is
Aconstant in direction
Bconstant in magnitude but not in direction
Cconstant in magnitude and direction
Dconstant neither in magnitude nor in direction.
Question 3 - Select One
In a non uniform circular motion, the acceleration on the particle is
Acentripetal acceleration only
Btangential acceleration only
Cthe resultant centripetal and tangential acceleration
Dcentrifugal acceleration

GRB PUBLICATION-VECTORS-OBJECTIVE QUESTIONS

Home
Ask Doubt
Profile