Water drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular ( equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops ?
The correct Answer is:(a) 89 cm; (b) 22 cm
To solve the problem step by step, we need to analyze the motion of the water drops falling from the shower nozzle. Here’s how we can approach the question:
Given Data:
- Height of the nozzle from the floor, h=200cm
- The drops fall at equal intervals of time.
- The first drop strikes the floor when the fourth drop begins to fall.
Step 1: Understand the Time Intervals
Let the time interval between the drops be T.
- The first drop takes 3T to reach the floor.
- The second drop takes 2T.
- The third drop takes T.
- The fourth drop is just about to fall.
Step 2: Use the Equation of Motion
We will use the equation of motion for free fall:
S=ut+12at2
Where:
- S is the displacement,
- u is the initial velocity (which is 0 for all drops),
- a is the acceleration due to gravity g (approximately 980cm/s2),
- t is the time.
For the first drop:
200=0⋅(3T)+12g(3T)2
This simplifies to:
200=12g(9T2)
200=9gT22
T2=4009g
Step 3: Calculate the Displacement for the Second and Third Drops
For the second drop:
S2=12g(2T)2
Substituting T2:
S2=12g(4T2)=2gT2
Substituting T2:
S2=2g(4009g)=8009cm≈88.89cm
For the third drop:
S3=12g(T)2
Substituting T2:
S3=12g(T2)=12g(4009g)=2009cm≈22.22cm
Final Answers:
(a) The distance of the second drop below the nozzle is approximately 88.89cm.
(b) The distance of the third drop below the nozzle is approximately 22.22cm.
- Height of the nozzle from the floor, h=200cm
- The drops fall at equal intervals of time.
- The first drop strikes the floor when the fourth drop begins to fall.
Let the time interval between the drops be T.
- The first drop takes 3T to reach the floor.
- The second drop takes 2T.
- The third drop takes T.
- The fourth drop is just about to fall.
We will use the equation of motion for free fall:
S=ut+12at2
Where:
- S is the displacement,
- u is the initial velocity (which is 0 for all drops),
- a is the acceleration due to gravity g (approximately 980cm/s2),
- t is the time.
200=0⋅(3T)+12g(3T)2
This simplifies to:
200=12g(9T2)
200=9gT22
T2=4009g
For the second drop:
S2=12g(2T)2
Substituting T2:
S2=12g(4T2)=2gT2
Substituting T2:
S2=2g(4009g)=8009cm≈88.89cm
S3=12g(T)2
Substituting T2:
S3=12g(T2)=12g(4009g)=2009cm≈22.22cm
(a) The distance of the second drop below the nozzle is approximately 88.89cm.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Single Correct Choice Type)54videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( More than One Correct Choice Type )6videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - Checkpoints5videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
Water drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g=9.8m/s2
View SolutionWater drops are falling from a nozzle of a shower onto the floor, from a height of 9.8 m. The drops fall at a regular interval of time. When the first drop strikes the floor, at that instant, the third drop begins to fall. Locate the position of second drop from the floor when the first drop strikes the floor.
View Solution
Knowledge Check
- Question 1 - Select One
Drops of water fall from the roof of a building 9m. High at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distance of the second and third drops from the roof?
A6 m and 2 mB6 m and 3 mC4 m and 1 mD4 m and 2 m - Question 2 - Select One
Water drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (take=g=10m−2)
A1.25 mB2.15 mC2.75 mD3.75 m - Question 3 - Select One
Water drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. (g=10ms−2)
A1.25mB2.50mC3.75mD4.00m
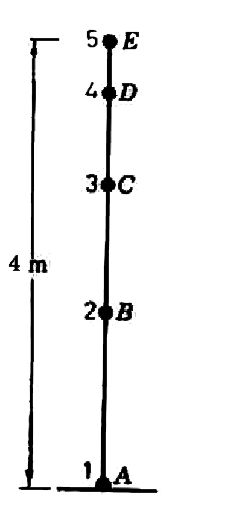
water drops trickle out from a nozzle and fall on the height 4.0 m below at regular intervals. When first drop reaches the floor, the fifth drop begins to fall. Find the positive of the drops , when a drop just strikes the floor.
 View Solution
View SolutionDrops of water from the roof of a house 6 m high fall at regular intervals. The first drop reaches the ground at an instant of time when third drop leaves the roof. Find the height of the second drop at that instant
View SolutionDrops of water fall at regular intervals from the roof of a building of height h=16m. The first drop striking the ground at the same moment as the fifth drop is ready to leave from the roof. Find the distance betweent he successive drops.
View SolutionWater drops are falling in regular intervals of time from top of a tower to height 9 m. If 4th drop begins to fall when 1st drop reaches the ground, find the positions of 2nd&3rd drops from the top of the tower.
View SolutionDrops of water fall at refular intervais from the roof of a building of height H = 5 m, the first drop strikes the ground at the same moment when the fifth drop detaches itself from the roof. Then ratio of distances first drop reaches the ground are :
View Solution

