Water is being poured in a vessel at a constant rate αm2/s. There is a small hole of area a at the bottom of the tank. The maximum level of water in the vessel is proportional to
α
α2
a−1
a−2
The correct Answer is:B, D
To solve the problem, we need to analyze the inflow and outflow of water in the vessel and establish the relationship between the maximum height of water (h) in the vessel, the rate of inflow (α), and the area of the hole (a).
1. Identify the Rate of Inflow:
The water is being poured into the vessel at a constant rate, denoted as α (in m2/s). This means the volume of water entering the vessel per unit time is given by:
Rate of inflow=α
2. Identify the Rate of Outflow:
The water exits through a small hole at the bottom of the vessel. The rate of outflow can be expressed using Torricelli's law, which states that the speed of efflux (v) of a fluid under the force of gravity through an orifice is given by:
v=√2gh
where g is the acceleration due to gravity and h is the height of the water column above the hole.
The rate of outflow (Q) can then be expressed as:
Rate of outflow=a⋅v=a⋅√2gh
3. Set Inflow Equal to Outflow:
At equilibrium, the rate of inflow equals the rate of outflow:
α=a⋅√2gh
4. Solve for h:
Rearranging the equation to solve for h:
√2gh=αa
Squaring both sides gives:
2gh=(αa)2
Now, isolating h:
h=α22ga2
5. Determine Proportional Relationships:
From the equation h=α22ga2, we can see that:
- h is directly proportional to α2 (the rate of inflow).
- h is inversely proportional to a2 (the area of the hole).
Conclusion:
The maximum level of water in the vessel is proportional to α2 and inversely proportional to a2.
Final Answer:
The maximum level of water h in the vessel is proportional to:
h∝α2a2
The water is being poured into the vessel at a constant rate, denoted as α (in m2/s). This means the volume of water entering the vessel per unit time is given by:
Rate of inflow=α
The water exits through a small hole at the bottom of the vessel. The rate of outflow can be expressed using Torricelli's law, which states that the speed of efflux (v) of a fluid under the force of gravity through an orifice is given by:
v=√2gh
where g is the acceleration due to gravity and h is the height of the water column above the hole.
Rate of outflow=a⋅v=a⋅√2gh
At equilibrium, the rate of inflow equals the rate of outflow:
α=a⋅√2gh
Rearranging the equation to solve for h:
√2gh=αa
Squaring both sides gives:
2gh=(αa)2
Now, isolating h:
h=α22ga2
From the equation h=α22ga2, we can see that:
- h is directly proportional to α2 (the rate of inflow).
- h is inversely proportional to a2 (the area of the hole).
The maximum level of water in the vessel is proportional to α2 and inversely proportional to a2.
The maximum level of water h in the vessel is proportional to:
h∝α2a2
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching
12 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A point source S is placed at a height h from the bottom of a vessel of height H(<h). The vessel is polished at the base. Water is polished at the base. Water is gradually filled in the vessel at a constant rate αm3/s. The distance d of image of the source after reflection from mirror from the bottom of the vessel varies with time t as
View SolutionThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View Solution
Knowledge Check
Water is poured into an empty cylindrical tank at a constant rate. In 10 minutes, the height of the water increased by 7 feet. The radius of the tank is 10 feet. What is the rate at which the water is poured?
A11π/8 cubic feet per minute.B11π/3 cubic feet per minute.C7π/60 cubic feet per minute.D70π cubic feet per minute.
A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cu m/min. Then, the rate (in m/min) at which the level of water is rising at the instant when the depth of water in the tank is 10 m is
View SolutionA tank has a hole at its bottom. The time needed to empty the tank from level h1 to h2 will be proportional to
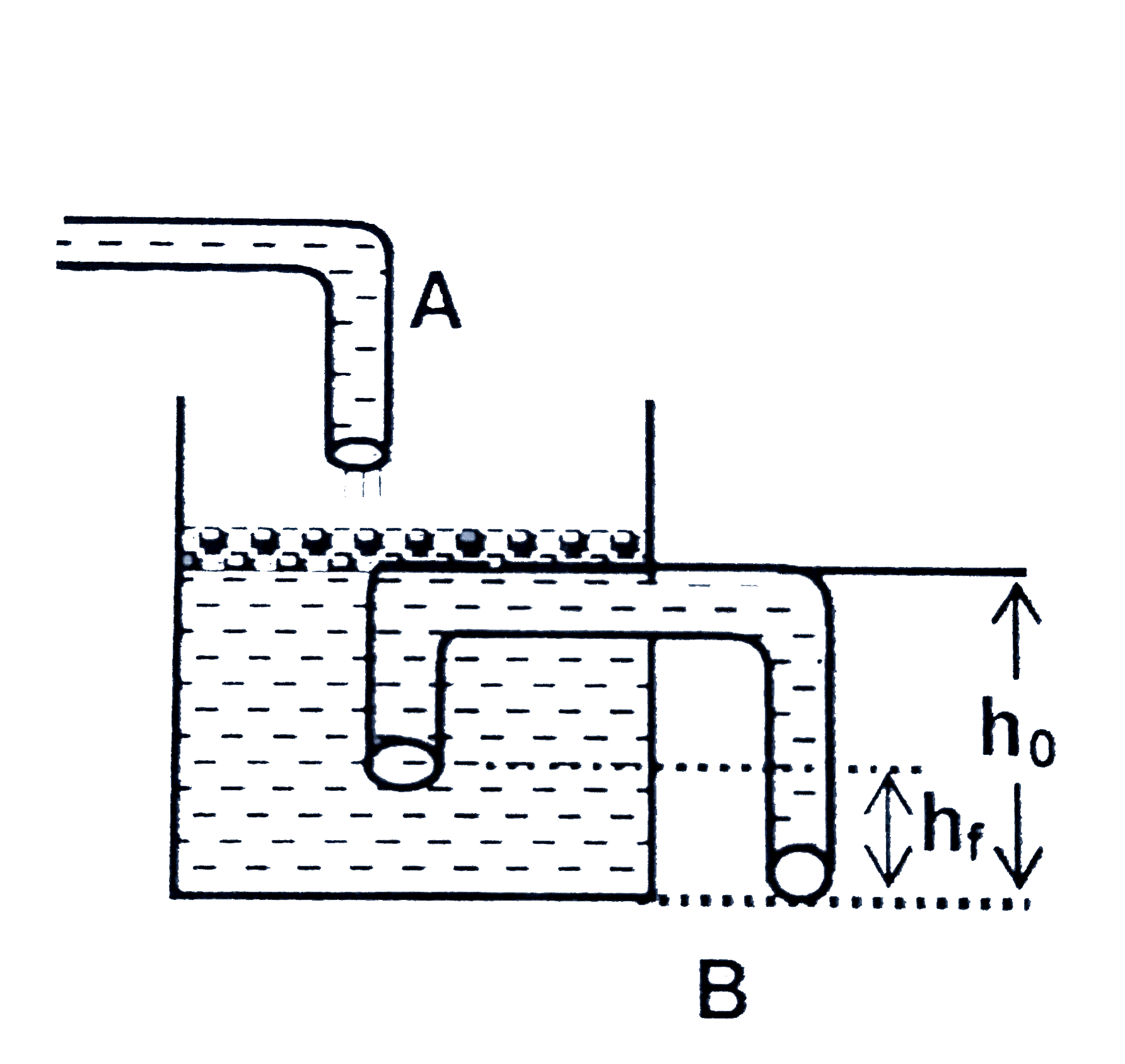
View SolutionIn the figure shown, water flows into the open vessel through pipe A at a constant rate. The water can flow out of the vessel by pipe B. The maximum flow-rate fo the water in pipe B is slightly more than that in pipe A. Final height of the water level in the vessel would be
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionWater flows into a large tank with flat bottom at the rate of 10−4m3s−1. Water is also leaking out of a hole of area 1 cm2 at its bottom. If the height of the water in the tank remains steady, then this height is :
View SolutionA cylindrical tank has a small hole at bottom. At t=0, a tap starts to supply water into the tank at a constant rate βm3/s.
(a) Find the maximum level of water Hmax in the tank ?
(b) At what time level of water becomes h(h<Hmax) Given a , area of hole, A : area of tank.
View Solution
