What displacement at an angle 60∘ to the x-axis has an x-component of 5m? ˆi and ˆj are unit vector in x and y directions, respectively.
5ˆi
5ˆi+5ˆj
5ˆi+5√3ˆj
All of the above
The correct Answer is:C
In first option (a), vector is along the x-axis (figure)
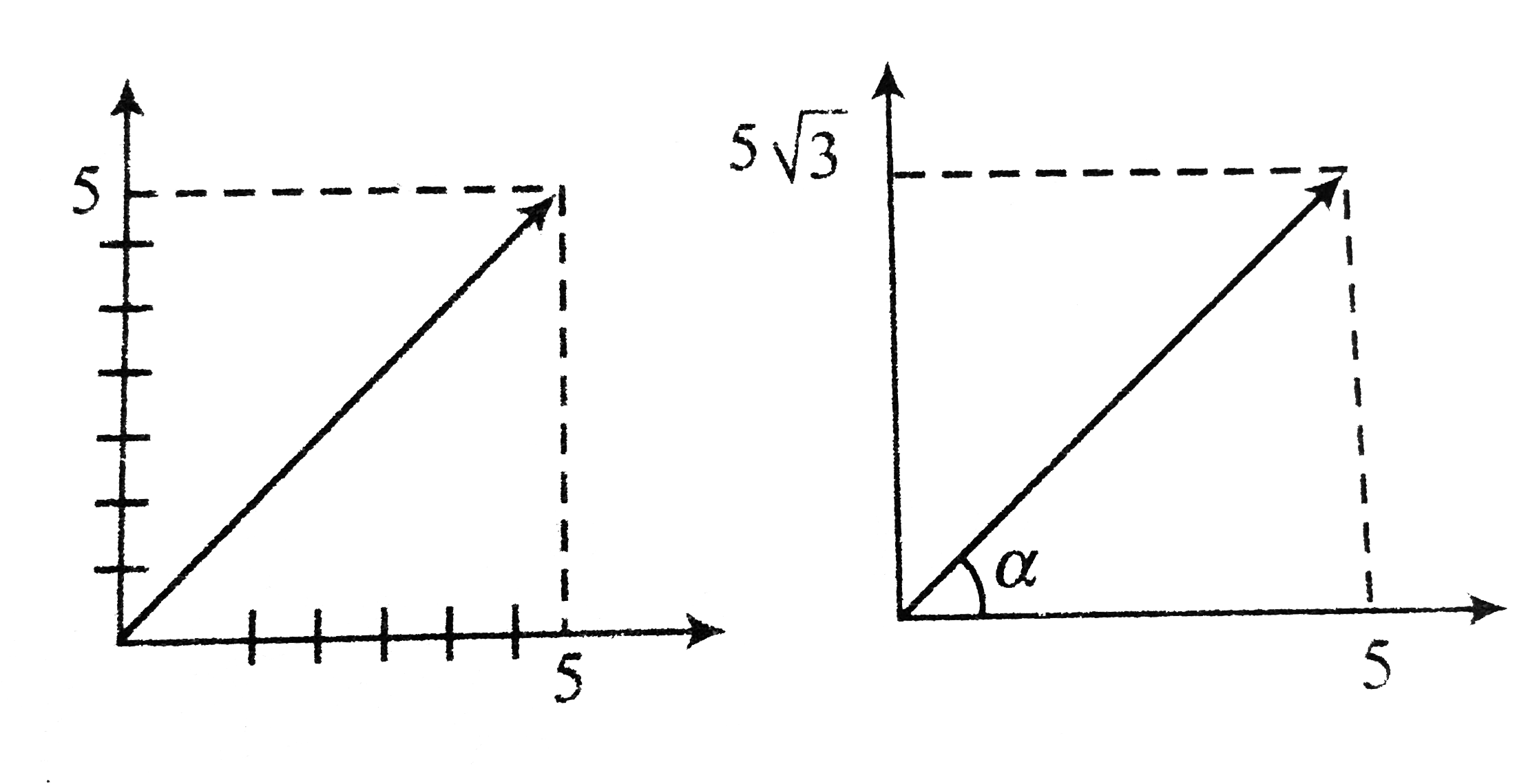
(b), angle of vector with the x-axis
tanθ=55=1⇒θ45∘
(C ),angle of vector with the x-axis
tanα=5√35=√3⇒α=5√35=√3⇒α=60∘
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Subjective
28 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
What displacement at an angle 60∘ to the x-axis has an x-component of 5 m? iandj are unit vectors in x and y directions, respectively.
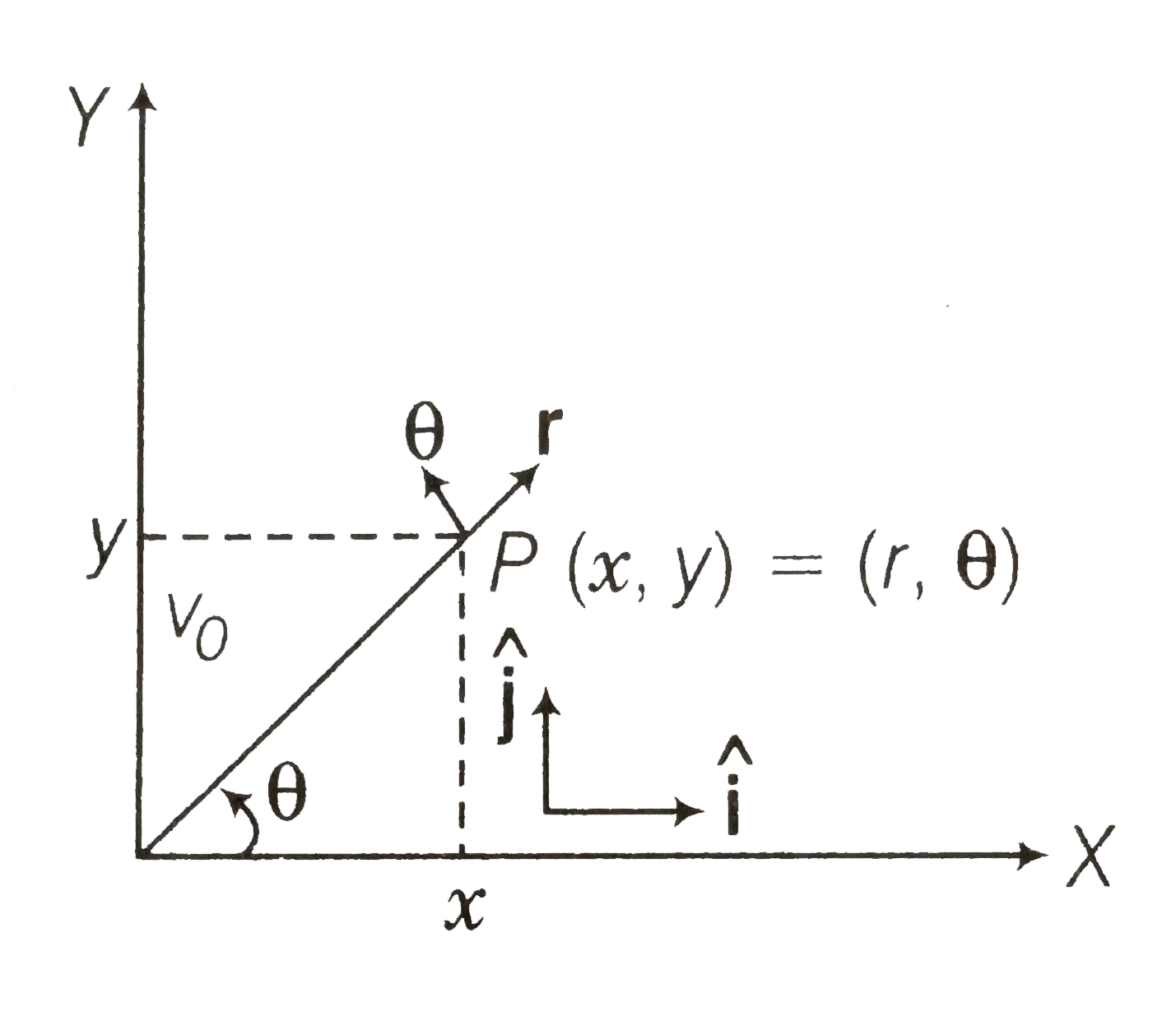
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=Axˆi+Ayˆj, where ˆi and ˆj are unit vector along x and y-directions, respectively and Ax and Ay are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A=Arˆr+Aθˆθ, where ˆr=rr=cosθˆi+sinθˆj and ˆθ=−sinθˆi+cosθˆj are unit vectors along direction in which r and θ are increasing.
(a) Express ˆi and ˆj in terms of ˆr and ˆθ.
(b) Show that both ˆr and ˆθ are unit vectors and are perpendicular to each other.
(c) Show that ddt(ˆr)=ωˆθ, where ω=dθdt and ddt(ˆθ)=−θˆr.
(d) For a particle moving along a spiral given by r=aθˆr, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View Solution
Knowledge Check
The angle which the vector →A=2ˆi+3ˆj makes with the y-axis, where ˆi and ˆj are unit vectors along x- and y-axis, respectively, is
Acos−1(3/5)Bcos−1(2/3)Ctan^(-1)(2//3)Dsin−1(2/3)The component of vector A=2ˆi+3ˆj along the vector ˆi+ˆj is
A5√2B10√2C5√2D5The unit vector along ˆi+ˆj is
AˆkBˆi+ˆjCˆi+ˆj√2Dˆi+ˆj2
The vector (ˆi+ˆj) is a unit vector.
View SolutionFind the value of x for which x(ˆi+ˆj+ˆk)is a unit vector.
View SolutionFind the value of x for which x (ˆi+ˆj+ˆk) is a unit vector.
View SolutionFind the values of 'x' for which x(ˆi+ˆj+ˆk) is a unit vector.
View SolutionWhat displacement must be added to the displacement 25ˆi−6ˆjm to give a displacement of 7.0 m pointing in the x-direction ?
View Solution
