What is magnetic dipole? Derive an expression for magnetic field intensity at a point on the equitorial line of a bar magnet.Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

Magnetic field intensity: Magnetic field intensity at a point on equitorial line of magnetic dipole: Let we have a bar magnet NS of length 2l. O is the mid-point of the bar magnet and m is the pole strength of, its each pole. Let P is any point on the equitorial line of this bar magnet passing through O. Let r= OP= Distance of observation point from centre of the magnets. Also SN = 2l= Magnetic length of magnet and OS= ON=l
Magnetic field at P due to North Pole $= B_{1} = \frac{μ_{0}}{4 π} \frac{m}{N P^{2}}$ along PA
In right angle $Δ O S P$ ,
$N P^{2} = O P^{2} + O N^{2} = r^{2} + l^{2}$
$\Rightarrow B_{1} = \frac{μ_{0} m}{4 π (r^{2} + l^{2})}$ along PA ...(i)
Magnetic field at P due to South Pole $= B_{2} = \frac{μ_{0}}{4 π} \frac{m}{S P^{2}}$ along PB
In right angled $Δ O S P$
$S P^{2} = O P^{2} + O S^{2} = r^{2} + l^{2}$
$\Rightarrow B_{2} = \frac{μ_{0}}{4 π} \frac{m}{(r^{2} + l^{2})}$ along PB...(ii)

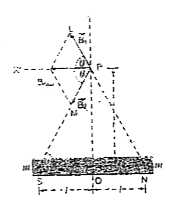
From (i) and (ii), it is clear that $B_{1} and B_{2}$ are equal in magnitude
Let $∠ P S N = ∠ P N S = θ$
Also $∠ A P X = ∠ P N S = θ$ (Corresponding angles) and $∠ X P S = ∠ P S N = θ$ -(alternate angles)
Now, components of ${\to B}_{1} and {\to B}_{2}$ along Y-axis are $B_{1} sin θ and B_{2} sin θ$ respectively. These two components are equal and opposite and hence, they cancel each other. While components of ${\to B}_{1} and {\to B}_{2}$ along X-axis are $B_{1} cos θ and B_{2} cos θ$ respectively. They act along the same direction and hence, are added up.
$∴$ The magnitude of resultant magnetic field at P due to bar magnet will be
$B = B_{1} cos θ + B_{2} cos θ$
$B = B_{1} cos θ + B_{1} cos θ (∵ B_{1} = B_{2}]$
$B = 2 B_{1} cos θ$
In right angled $Δ O P S$
$cos θ = \frac{O S}{S P}$
But $S P^{2} = O S^{2} + O P^{2}$ [Using Pythagorous Theorem]
$S P = \sqrt{O S^{2} + O P^{2}}$
$\Rightarrow cos θ = \frac{O S}{\sqrt{O S^{2} + O P^{2}}}$
$\Rightarrow cos θ = \frac{l}{\sqrt{l^{2} + r^{2}}}$ ...(iv)
Use eqns (i) and (iv) in eq (iii), $B = 2 \frac{μ_{0}}{4 π} \frac{m}{(r^{2} + l^{2})} . \frac{l}{\sqrt{r^{2} + l^{2}}}$
$\Rightarrow B = 2 \frac{μ_{0}}{4 π} \frac{m (2 l)}{{(r^{2} + l^{2})}^{3 / 2}}$
But m (2l)= M =Magnetic moment
$∴ B = \frac{μ_{0}}{4 π} \frac{M}{{(r^{2} + l^{2})}^{3 / 2}}$
If observation point P is far away from the magnet ie., $r > > l$ or we can say than when magnet is of very short length. Thus $l^{2}$ can be neglected.
$B = \frac{μ_{0}}{4 π} \frac{M}{{(r^{2})}^{3 / 2}}$
$B = \frac{μ_{0}}{4 π} \frac{M}{(r^{3})}$
which is the required expression for magnetic field at any point on the equitorial line of bar magnet. Direction of magnetic field at a point on the equitorial line of magnetic dipole is opposite to direction of magnetic dipole moment.

|

Updated on:21/07/2023

Class 12 PHYSICS MAGNETIC DIPOLES AND EARTH'S MAGNETISM

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-MAGNETIC DIPOLES AND EARTH'S MAGNETISM-Short Answer Type Questions

Home
Ask Doubt
Profile