What is the condition under which Hooke's law holds goods?
To determine the condition under which Hooke's law holds good, we can follow these steps:
1. Understanding Hooke's Law:
Hooke's law states that the stress (σ) produced in a material is directly proportional to the strain (ε) developed in that material. Mathematically, this can be expressed as:
σ=E⋅ϵ
where E is the modulus of elasticity (the constant of proportionality).
2. Defining Stress and Strain:
- Stress (σ) is defined as the force applied per unit area.
- Strain (ε) is defined as the deformation (change in length/original length) of the material.
3. Identifying the Proportionality:
The relationship between stress and strain is linear within certain limits. This means that as stress increases, strain increases proportionally.
4. Elastic Limit:
Hooke's law holds good only within the elastic limit of the material. The elastic limit is the maximum extent to which a material can be deformed without undergoing permanent deformation. Beyond this limit, the material may not return to its original shape, and Hooke's law no longer applies.
5. Proportional Limit:
The elastic limit is sometimes also referred to as the proportional limit, where the stress-strain relationship remains linear.
Conclusion:
Hooke's law holds good within the elastic limit or proportional limit of the material.
---
Hooke's law states that the stress (σ) produced in a material is directly proportional to the strain (ε) developed in that material. Mathematically, this can be expressed as:
σ=E⋅ϵ
where E is the modulus of elasticity (the constant of proportionality).
- Stress (σ) is defined as the force applied per unit area.
- Strain (ε) is defined as the deformation (change in length/original length) of the material.
The relationship between stress and strain is linear within certain limits. This means that as stress increases, strain increases proportionally.
Hooke's law holds good only within the elastic limit of the material. The elastic limit is the maximum extent to which a material can be deformed without undergoing permanent deformation. Beyond this limit, the material may not return to its original shape, and Hooke's law no longer applies.
The elastic limit is sometimes also referred to as the proportional limit, where the stress-strain relationship remains linear.
Hooke's law holds good within the elastic limit or proportional limit of the material.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)VERY SHORT ANSWER QUESTIONS8videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)FROM YOUNG.S MODULUS19videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)LONG ANSWER QUESTIONS5videos
PROPERTIES OF MATTER
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D12videos
SAMPLE QUESTION PAPER - 01
Similar Questions
Knowledge Check
- Question 1 - Select One
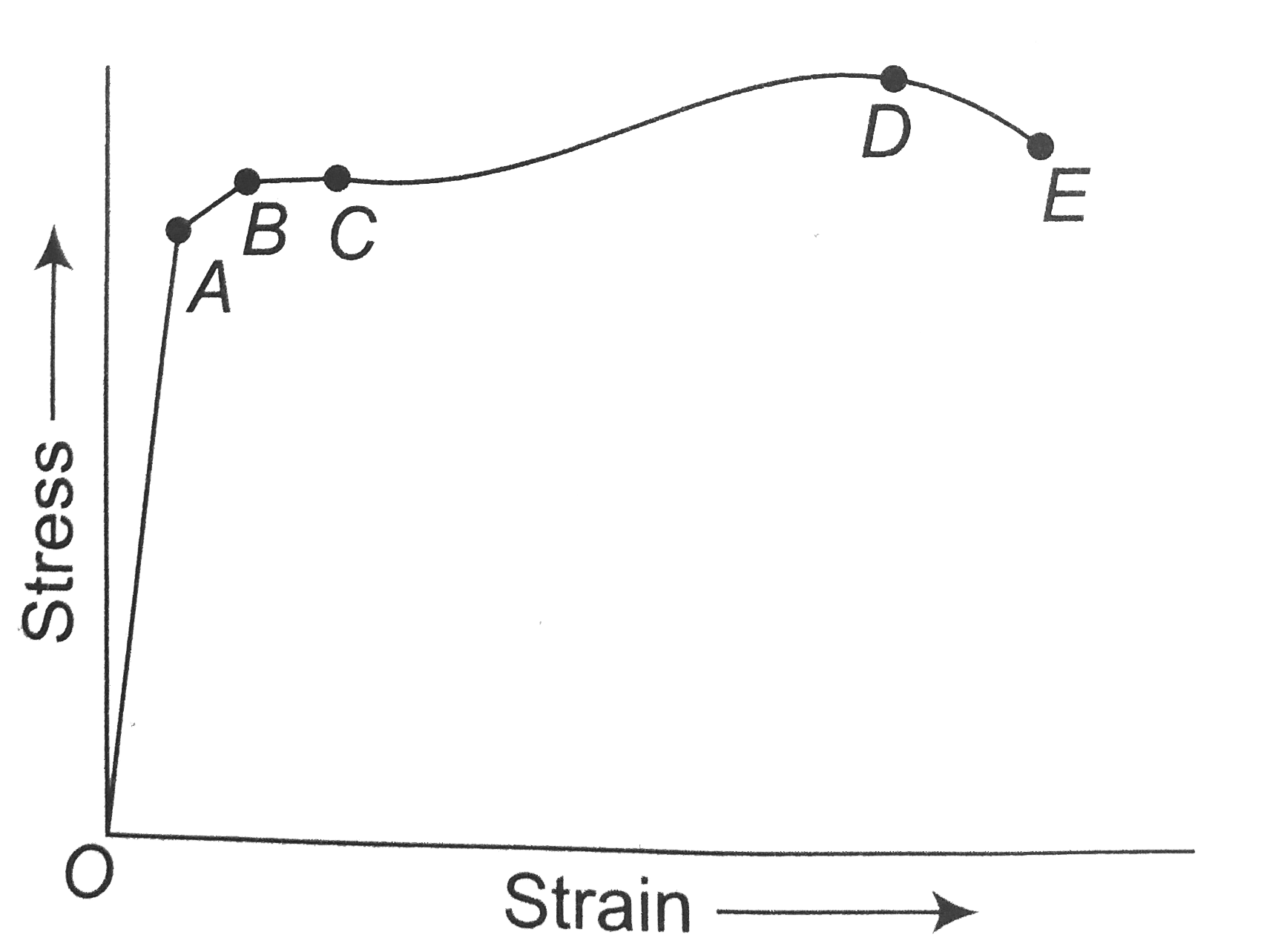
The stress strain graph for a metal wire is as shown in the figure. In the graph, the region in which Hooke's law is obeyed, the ultimate strength and fracture are represented byAOA, C, DBOB, D, ECÂ OA, D, EDOB, C, D - Question 2 - Select One
What are the conditions for an ideal solution which obeys Raoult's law over the entire range of concentration ?
AΔmixH=0,ΔmixV=0,PTotal=p∘AxA+p∘BxBBΔmixH=+ve,ΔmixV=0,PTotal=p∘AxA+p∘BxBCΔmixH=0,ΔmixV=+ve,PTotal=p∘AxA+p∘BxBDΔmixH=0,ΔmixV=0,PTotal=p∘BxB
Show that the Young.s modulus of the material of a wire is equal to the stress required to double the initial length of the wire. Assume that Hookes law holds good throughout the process.
View Solution(i) State Hook's law.
(ii) Draw a labelled graph of tensile stress against tensile strain for a metal wire upto the breaking point. Shhow on your graph the region in which Hooke's law is obeyed.
What is the significance of the area between the graph and the strain axis withing the Hooke's law region?View SolutionThe conditions under which transpiration would be most rapid are
View SolutionThe distance upto which ray optics holds good is called
View SolutionIf a,b,c,d,e are positive numbers, then which of the following holds good
View SolutionAssertion:- Materials can be stretched even beyond proportionality limit. (point till which Hooke's law is valid is called proportionality limit)
Reason:- Elastic forces can be conservative even beyond proportional limit.View Solution

