What is the difference between tensile stress and volume stress?
To understand the difference between tensile stress and volume stress, let's break it down step by step.
Step 1: Define Tensile Stress
Tensile stress is defined as the force that causes an object to stretch or elongate. It is calculated as the force applied per unit area of the cross-section of the object.
Formula:
Tensile Stress(σt)=FA
Where:
- F = Deforming force (in Newtons)
- A = Cross-sectional area (in square meters)
Step 2: Explain the Effect of Tensile Stress
When a tensile stress is applied to an object (like a rod), it results in an increase in the length of that object. For example, if a rod is pulled from both ends, its length increases due to the tensile stress acting along its length.
Step 3: Define Volume Stress
Volume stress, on the other hand, is the stress that results from forces applied uniformly in all directions, causing a change in the volume of the object.
Formula:
Volume Stress(σv)=FV
Where:
- F = Deforming force (in Newtons)
- V = Volume of the object (in cubic meters)
Step 4: Explain the Effect of Volume Stress
When volume stress is applied, it affects the object uniformly from all sides, leading to a change in volume rather than length. For instance, if a cube is compressed from all sides, its volume decreases due to the volume stress applied.
Step 5: Summarize the Differences
- Direction of Force: Tensile stress is unidirectional (along one dimension), while volume stress is multidirectional (applied from all dimensions).
- Effect on Object: Tensile stress results in a change in length, whereas volume stress results in a change in volume.
Conclusion
In summary, tensile stress and volume stress are two different types of mechanical stress that affect materials in distinct ways. Tensile stress leads to elongation, while volume stress leads to compression.
---
Tensile stress is defined as the force that causes an object to stretch or elongate. It is calculated as the force applied per unit area of the cross-section of the object.
Tensile Stress(σt)=FA
Where:
- F = Deforming force (in Newtons)
- A = Cross-sectional area (in square meters)
When a tensile stress is applied to an object (like a rod), it results in an increase in the length of that object. For example, if a rod is pulled from both ends, its length increases due to the tensile stress acting along its length.
Volume stress, on the other hand, is the stress that results from forces applied uniformly in all directions, causing a change in the volume of the object.
Volume Stress(σv)=FV
Where:
- F = Deforming force (in Newtons)
- V = Volume of the object (in cubic meters)
When volume stress is applied, it affects the object uniformly from all sides, leading to a change in volume rather than length. For instance, if a cube is compressed from all sides, its volume decreases due to the volume stress applied.
- Direction of Force: Tensile stress is unidirectional (along one dimension), while volume stress is multidirectional (applied from all dimensions).
- Effect on Object: Tensile stress results in a change in length, whereas volume stress results in a change in volume.
In summary, tensile stress and volume stress are two different types of mechanical stress that affect materials in distinct ways. Tensile stress leads to elongation, while volume stress leads to compression.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)VERY SHORT ANSWER QUESTIONS
8 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)FROM YOUNG.S MODULUS
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)LONG ANSWER QUESTIONS
5 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Tensile stress is possible in
View SolutionWhat is the dimensional formula of tensile stress?
View SolutionWhat is the dimensional formula of tensile stress?
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
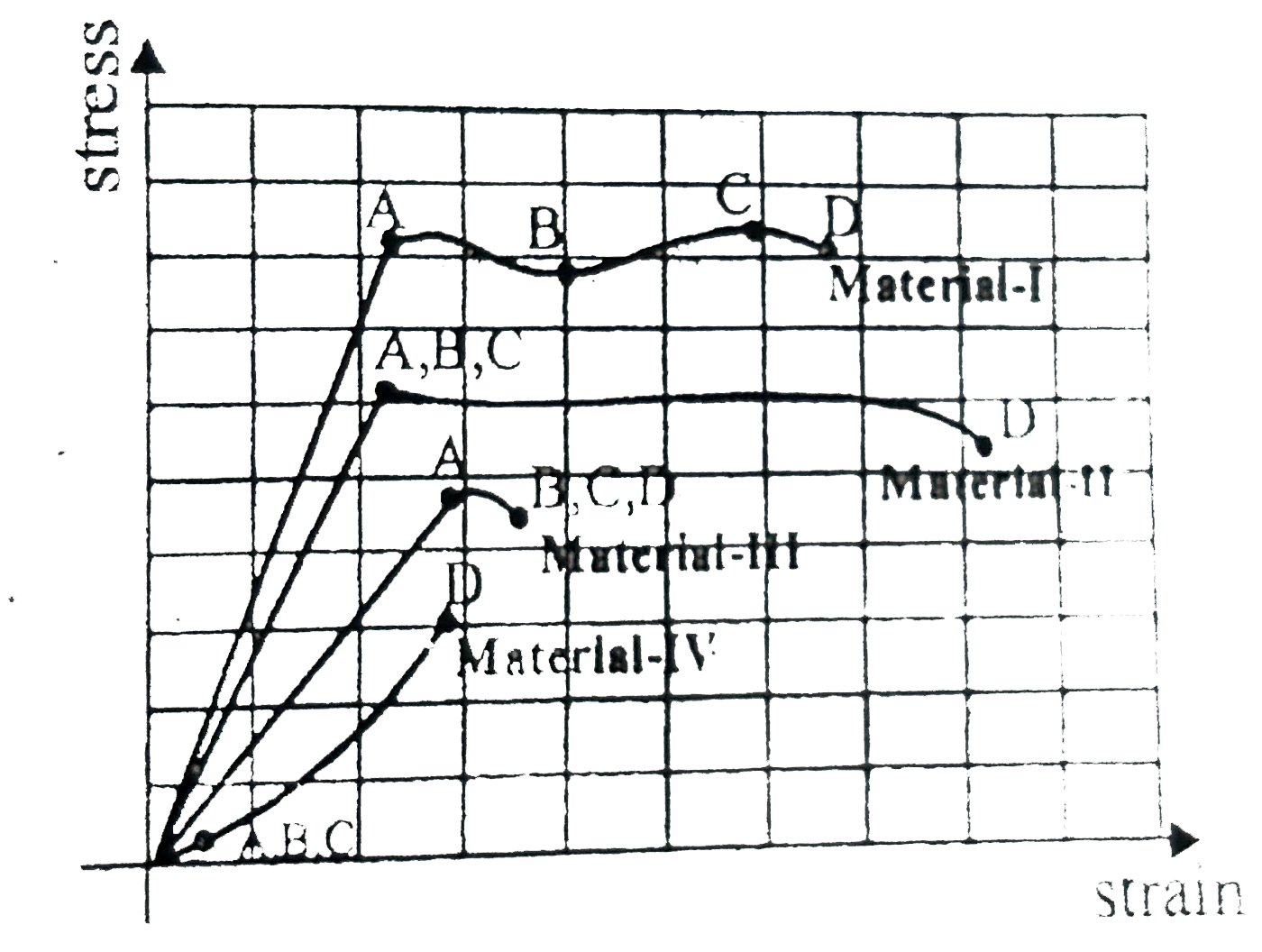
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionWhat is thermal stress?
View SolutionDefine stress and strain?
View Solution(i) State Hook's law.
(ii) Draw a labelled graph of tensile stress against tensile strain for a metal wire upto the breaking point. Shhow on your graph the region in which Hooke's law is obeyed.
What is the significance of the area between the graph and the strain axis withing the Hooke's law region?
View Solution
