What is the fractional decrease in kinetic energy of a body of mass m1 when it makes a head on elastic collision with another body of mass m2 kept at rest?
The correct Answer is:A, B, D
To find the fractional decrease in kinetic energy of a body of mass m1 when it makes a head-on elastic collision with another body of mass m2 that is at rest, we can follow these steps:
Step 1: Understand the Initial and Final Kinetic Energy
The initial kinetic energy (Ki) of the body of mass m1 before the collision is given by:
Ki=12m1v21
where v1 is the initial velocity of mass m1.
The body of mass m2 is at rest, so its initial kinetic energy is:
Ki2=0
Step 2: Determine the Final Velocities After Collision
In an elastic collision, both momentum and kinetic energy are conserved. The final velocity of mass m1 after the collision (v′1) and the final velocity of mass m2 after the collision (v′2) can be calculated using the following formulas:
v′1=(m1−m2)(m1+m2)v1
v′2=2m1(m1+m2)v1
Step 3: Calculate the Final Kinetic Energy
The final kinetic energy (Kf) of mass m1 after the collision is:
Kf1=12m1(v′1)2=12m1((m1−m2)(m1+m2)v1)2
The final kinetic energy of mass m2 after the collision is:
Kf2=12m2(v′2)2=12m2(2m1(m1+m2)v1)2
Step 4: Combine the Final Kinetic Energies
The total final kinetic energy after the collision is:
Kf=Kf1+Kf2=12m1((m1−m2)(m1+m2)v1)2+12m2(2m1(m1+m2)v1)2
Step 5: Calculate the Fractional Decrease in Kinetic Energy
The fractional decrease in kinetic energy is given by:
Fractional Decrease=Ki−KfKi
Substituting the values of Ki and Kf:
Fractional Decrease=12m1v21−Kf12m1v21
Step 6: Simplify the Expression
After simplifying the expression, we find:
Fractional Decrease=1−m2m1+m2(v′1v1)2
Substituting v′1 from earlier, we can derive the final expression:
Fractional Decrease=4m1m2(m1+m2)2
Final Answer
Thus, the fractional decrease in kinetic energy of the body of mass m1 when it makes a head-on elastic collision with another body of mass m2 at rest is:
4m1m2(m1+m2)2
The initial kinetic energy (Ki) of the body of mass m1 before the collision is given by:
Ki=12m1v21
where v1 is the initial velocity of mass m1.
Ki2=0
In an elastic collision, both momentum and kinetic energy are conserved. The final velocity of mass m1 after the collision (v′1) and the final velocity of mass m2 after the collision (v′2) can be calculated using the following formulas:
v′1=(m1−m2)(m1+m2)v1
v′2=2m1(m1+m2)v1
The final kinetic energy (Kf) of mass m1 after the collision is:
Kf1=12m1(v′1)2=12m1((m1−m2)(m1+m2)v1)2
The final kinetic energy of mass m2 after the collision is:
Kf2=12m2(v′2)2=12m2(2m1(m1+m2)v1)2
The total final kinetic energy after the collision is:
Kf=Kf1+Kf2=12m1((m1−m2)(m1+m2)v1)2+12m2(2m1(m1+m2)v1)2
The fractional decrease in kinetic energy is given by:
Fractional Decrease=Ki−KfKi
Fractional Decrease=12m1v21−Kf12m1v21
After simplifying the expression, we find:
Fractional Decrease=1−m2m1+m2(v′1v1)2
Substituting v′1 from earlier, we can derive the final expression:
Fractional Decrease=4m1m2(m1+m2)2
Thus, the fractional decrease in kinetic energy of the body of mass m1 when it makes a head-on elastic collision with another body of mass m2 at rest is:
4m1m2(m1+m2)2
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.5
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
In a head on elastic collision of two bodies of equal masses
View SolutionCalculate the kinetic energy of a body of mass 2 kg moving with speed of 10 m s−1
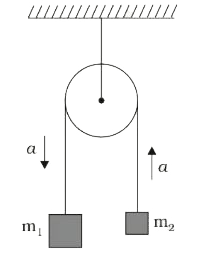
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
View SolutionFind the kinetic energy of a body of mass 1 kg moving with a uniform velocity of 10 ms−1
View SolutionA particle of mass m1, makes a head on elastic collision with another stationary body of mass m2 If m1, rebounds with half of its original speed then (m1m2) is
View SolutionA particle moving with kinetic energy E makes a head on elastic collision with an identical particle at rest. During the collision
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionMaximum energy transfer for an elastic collision will occur if one body is at rest when
View SolutionA particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
View SolutionA particle of mass m, kinetic energy K and momentum p collides head on elastically with another particle of mass 2m at rest. After collision, :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9(t)None
View Solution
