What is the magnetic field along the axis and equatorial line of a bar magnet ? Solution in Tamil

Video Solution

Text Solution

Verified by Experts

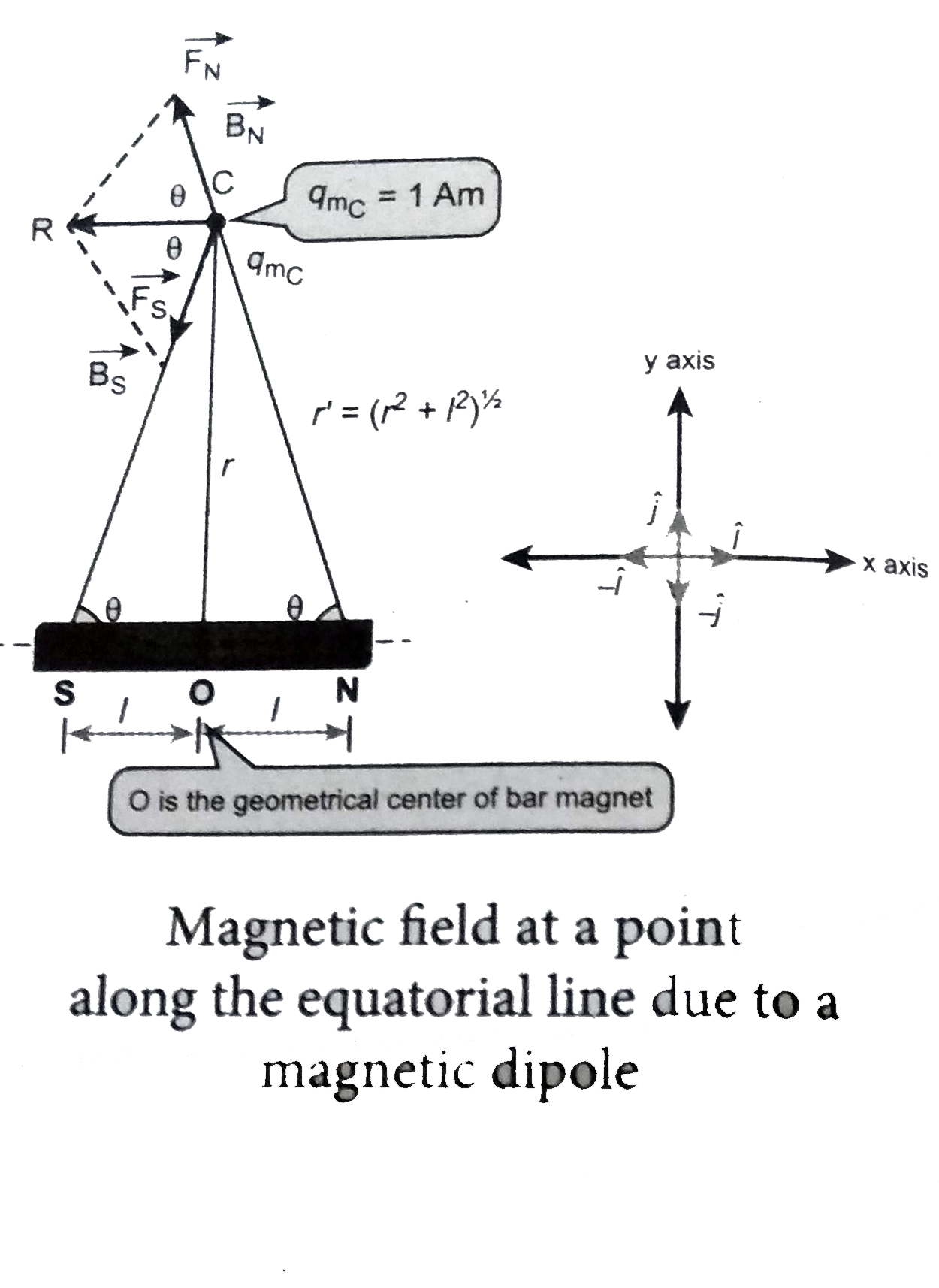
Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet) Consider a bar magnet NS. Let N be the north pole and be the south pole of the bar magnet, each with pole strength $q_{m}$ and separated by a distance of 2l. The magnetic field (lies along the equatorial line) at a distance r from the geometrical center of the bar mao can be computed by keeping unit north pole $(q_{m} C = 1 A m)$ at C. The force experience the unit north pole at C due to pole strength N-S can be computed using Coulomb.s law of magnetism as follows:
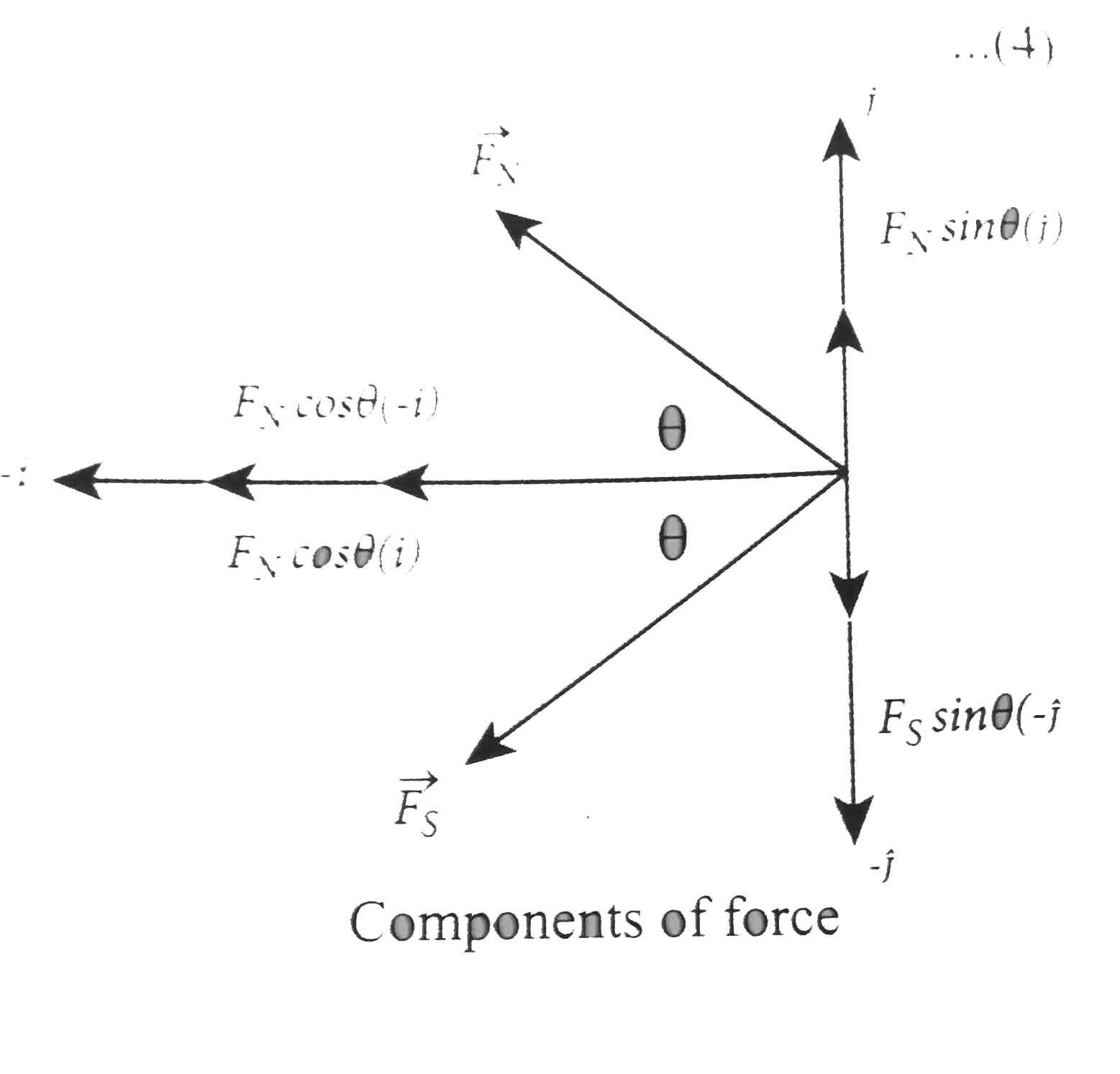
The force of. repulsion between North Pole of the bar magnet and unit north pole at point (in free space) is $\to F = - F_{N} cos θ ˆ i + F_{N} sin θ ˆ j$

Where $F_{N} = \frac{μ_{0} q_{m}}{4 π r^{1 / 2}}$
The force of attraction (in free space) between south pole of the bar magnet and unit north pole at point C
$\to s = - F_{S} cos θ ˆ i - F_{s} sin θ j$ .......(2)
Where $F_{S} = \frac{μ_{0} q_{m}}{4 π r^{1 / 2}}$
From equation (1) and equation (2), the net force at point Cis $\to F = {\to F}_{N} + F_{s}$ . This net force is equal to the magnetic field at the point C.
$\to B = - \frac{2 μ_{0}}{4 π} \frac{q_{m}}{r ’^{2}} cos θ ˆ i = - \frac{2 μ_{0}}{4 π} \frac{q_{m}}{(r^{2} + l^{2}) cos θ ˆ i}$
In a right angle triangle NOC as shown in the Figure 1 $cos θ = \frac{a d j a c e n t}{h y p o t e ν s e} = \frac{1}{r ’} = \frac{1}{{(r^{2} + l^{2})}^{\frac{1}{2}}}$
Substituting equation 4 in equation 3 we get
$\to B = - \frac{μ_{0} q_{m} \times (2 l)}{4 π_{{(r^{2} + l^{2})}^{\frac{3}{2}}}^{\frac{3}{2}} ˆ i}$ ......(5)
Since, magnitude of magnetic dipole moment is $∣ ∣ {\to P}_{m} ∣ ∣ = P_{m} = q_{m} .2 l$ and substituting in equation (5), the magnetic field at a point C
${\to B}_{e q u a \to r i a l} = - \frac{μ_{0}}{4 π} \frac{P_{m}}{{(r^{2} + l^{2})}^{\frac{3}{2}}} ˆ i$ ......(6)
compared to the distance between geometrical center of bar magnet and the location of point Ci.e.,r>>, then,
${(r^{2} + l^{2})}^{\frac{3}{2}} = r^{3}$ ...(7).

Therefore, using equation (7) in equation (6), we get
${\to B}_{e q u a \to r i a l} = - \frac{μ_{0}}{4 π} \frac{P_{m}}{r^{3}} ˆ i$
Since $P_{m} ˆ i = {\to P}_{m}$ , in general, the magnetic field at equatorial point is given by
${\to B}_{e q u a \to r i a l} = - \frac{μ_{0}}{4 π} \frac{P_{m}}{r^{3}}$ .......(8)
Note that magnitude of Barial is twice that of magnitude of $B_{e q u a \to r i a l}$ and the direction of $B_{a ξ a l}$ and $B_{e q u a \to r i a l}$ are opposite.

Updated on:21/07/2023

|

Class 12 PHYSICS SAMPLE PAPER-05 ( SOLVED )

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER-05 ( SOLVED ) -PART - IV

Home
Ask Doubt
Profile