What is the magnetic moment of an electron orbiting in a circular orbit of radius r with a speed v?
evr2
evr
er2v
None of these
The correct Answer is:A
To find the magnetic moment of an electron orbiting in a circular orbit of radius r with speed v, we can follow these steps:
Step 1: Understand the Formula for Magnetic Moment
The magnetic moment M of a current loop is given by the formula:
M=n⋅I⋅A
where:
- n is the number of turns in the loop,
- I is the current,
- A is the area of the loop.
Step 2: Determine the Current I
The current I can be defined as the charge passing through a point per unit time. For an electron, the charge Q is equal to the elementary charge e. The time T taken for one complete revolution (the period) can be calculated as:
T=DistanceVelocity=2πrv
Thus, the current I can be expressed as:
I=QT=eT=e2πrv=e⋅v2πr
Step 3: Calculate the Area A
The area A of the circular orbit is given by:
A=πr2
Step 4: Substitute Values into the Magnetic Moment Formula
Now we can substitute the values of n, I, and A into the magnetic moment formula:
- Since the electron is making one complete turn, n=1.
- We already found I=e⋅v2πr.
- The area A=πr2.
Thus, we have:
M=n⋅I⋅A=1⋅(e⋅v2πr)⋅(πr2)
Step 5: Simplify the Expression
Now, simplifying the expression:
M=e⋅v2πr⋅πr2=e⋅v⋅r2
Final Result
The magnetic moment M of the electron orbiting in a circular orbit of radius r with speed v is:
M=e⋅v⋅r2
The magnetic moment M of a current loop is given by the formula:
M=n⋅I⋅A
where:
- n is the number of turns in the loop,
- I is the current,
- A is the area of the loop.
The current I can be defined as the charge passing through a point per unit time. For an electron, the charge Q is equal to the elementary charge e. The time T taken for one complete revolution (the period) can be calculated as:
T=DistanceVelocity=2πrv
Thus, the current I can be expressed as:
I=QT=eT=e2πrv=e⋅v2πr
The area A of the circular orbit is given by:
A=πr2
Now we can substitute the values of n, I, and A into the magnetic moment formula:
- Since the electron is making one complete turn, n=1.
- We already found I=e⋅v2πr.
- The area A=πr2.
M=n⋅I⋅A=1⋅(e⋅v2πr)⋅(πr2)
Now, simplifying the expression:
M=e⋅v2πr⋅πr2=e⋅v⋅r2
The magnetic moment M of the electron orbiting in a circular orbit of radius r with speed v is:
M=e⋅v⋅r2
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPER 2017BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
Knowledge Check
A satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2The period of a satellite in a circular orbit of radius R is T. What is the period of another satellite in a circular orbit of radius 4 R ?
A4 TBT/8CT/4D8 T
Magnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
View SolutionA satellite X moves round the earth in a circular orbit of radius R. If another satellite Y of the same mass moves round the earth in a circular orbit of radius 4R, then the speed of X is ____________ times that of Y.
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
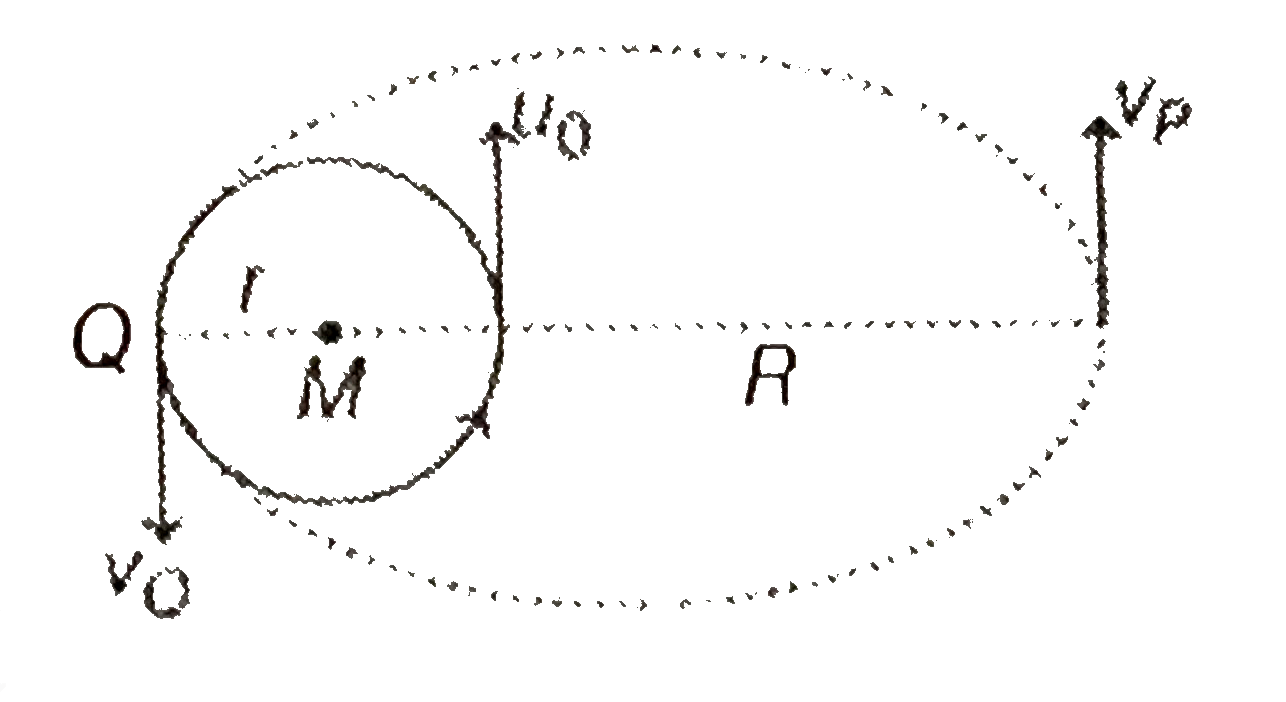
View SolutionDeduce an expression for the magnetic dipole moment of an electron orbiting around the central nucleus.
View SolutionThe de Broglie wavelength of an electron moving in a circular orbit is λ . The minimum radius of orbit is :
View Solution
