What is the pressure drop (in mm Hg) in the blood as it passes through a capillary 1mm long and 2μm in radius if the speed of the blood through the centre of the capillary is 0.66mms? (The viscosity of whole blood is 4×10−3PI)
The correct Answer is:A
To solve the problem of finding the pressure drop in the blood as it passes through a capillary, we can use the formula derived from Poiseuille's law for viscous flow in a cylindrical pipe. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the given values
- Length of the capillary (L) = 1 mm = 1×10−3 m
- Radius of the capillary (R) = 2 µm = 2×10−6 m
- Speed of blood (V_max) = 0.66 mm/s = 0.66×10−3 m/s
- Viscosity of blood (η) = 4×10−3Pa.s
Step 2: Use the formula for pressure drop
The pressure drop (ΔP) across a length of capillary can be calculated using the formula:
ΔP=8ηLVmaxR2
This formula is derived from Poiseuille's law for laminar flow in a cylindrical tube.
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
ΔP=8×(4×10−3)×(1×10−3)×(0.66×10−3)(2×10−6)2
Step 4: Calculate the denominator
Calculating the denominator:
(2×10−6)2=4×10−12
Step 5: Calculate the numerator
Calculating the numerator:
8×(4×10−3)×(1×10−3)×(0.66×10−3)=8×4×0.66×10−9=21.12×10−9
Step 6: Calculate the pressure drop
Now substituting the values into the equation:
ΔP=21.12×10−94×10−12=5.28×103Pa
Step 7: Convert pressure drop to mm Hg
To convert the pressure from Pascals to mm Hg, we use the conversion factor:
1mm Hg=133.322Pa
Thus,
ΔP (in mm Hg)=5.28×103133.322≈39.6mm Hg
Step 8: Final Answer
The pressure drop in the blood as it passes through the capillary is approximately 39.6 mm Hg.
---
- Length of the capillary (L) = 1 mm = 1×10−3 m
- Radius of the capillary (R) = 2 µm = 2×10−6 m
- Speed of blood (V_max) = 0.66 mm/s = 0.66×10−3 m/s
- Viscosity of blood (η) = 4×10−3Pa.s
The pressure drop (ΔP) across a length of capillary can be calculated using the formula:
ΔP=8ηLVmaxR2
This formula is derived from Poiseuille's law for laminar flow in a cylindrical tube.
Substituting the known values into the formula:
ΔP=8×(4×10−3)×(1×10−3)×(0.66×10−3)(2×10−6)2
Calculating the denominator:
(2×10−6)2=4×10−12
Calculating the numerator:
8×(4×10−3)×(1×10−3)×(0.66×10−3)=8×4×0.66×10−9=21.12×10−9
Now substituting the values into the equation:
ΔP=21.12×10−94×10−12=5.28×103Pa
To convert the pressure from Pascals to mm Hg, we use the conversion factor:
1mm Hg=133.322Pa
Thus,
ΔP (in mm Hg)=5.28×103133.322≈39.6mm Hg
The pressure drop in the blood as it passes through the capillary is approximately 39.6 mm Hg.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct
49 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Flow rate of blood through a capillary of cross - sectional are of 0.25m2 is 100cm3/s. The velocity of flow of blood iis
View SolutionIn giving a patient blood transfusion the bottle is set up so that the level of blood is 1.3 m above the needle which has an internal diameter of 0-36 mm, and is 0-03 m in length. If 4-5 ce of blood passes through the needle in one minute calculate the viscosity of blood if density is 1020kgm−3
View SolutionA liquid of density 900 kg/m3 is filled in a cylindrical tank open from top of upper radius 0.9 m and lower radius 0.3 m. A capillary tube of length l is attached at the bottom of the tank as shown in the figure. The capillary has outer radius 0.002 m and inner radius a.
When pressure p is applied at the top of the tank volume flow rate of the liquid is 8×10−6m3/s and if capillary tube is detached, the liquid comes out from the tank with a velocity 10 m/s
[Given : πa2=10−6m2anda2/1=2×10−6m]
Determine the coefficient of viscosity in SI units when the capillary tube is attached :
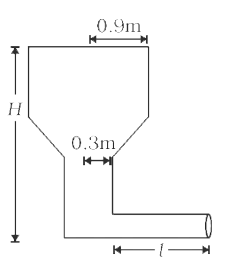
View SolutionThe flow of blood in a large artery of an anaeshetized dog is diverted through a venturimeter. The wider part of the meter has a cross sectional area equal to that of the artery i.e. 8mm2. The narrower parts has an are 4mm2. The pressure dorp in the artery is 24Pa. what is the speed of the blood in the artery ? Given that density of the blood = 1.06×103kg/m3
View SolutionThe capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5×10−2Nm−1.

View SolutionA rain drop of radius 0.3 mm falls through air with a terminal viscosity of 1ms−1. The viscosity of air is 18×10−5 poise. The viscous force on the rain drop is
View SolutionDuring blood transfusion the needle is inserted in a vein where the gauge pressure is 2000Pa . At what height must the blood container be placed so that blood may just enter the vein? Density of whole blood = 1.06×103Kg/m3.
View SolutionA glass rod of diameter d1=1.5mm in inserted symmetrically into a glass capillary with inside diameter d2=2.0 mm. Then the whole arrangement is vertically oriented and brought in contact with the surface of water. To what height will the liquid rise in the capillary?
Surface tension of water =73×10−3N/m
View SolutionVisible light passing through a circular hole forms a diffraction disc of radius 0.1 mm on a screen. If X-ray is passed through the same set-up, the radius of the diffraction disc will be
View SolutionThe average human heart forces four litre of blood per minute through arteries a pressure of 125 mm. If the density of blood is 1.03×103kg/m3 then the power of heart is :
View Solution
