A uniform rod AB, 4m long and weighing 12 kg, is supported at end A, with a 6 kg lead weight at B. The rod floats as shown in figure with one-half of its length submerged. The buoyant force on the lead mass is negligible as it is of negligible volume. Find the tension in the cord and the total volume of the rod
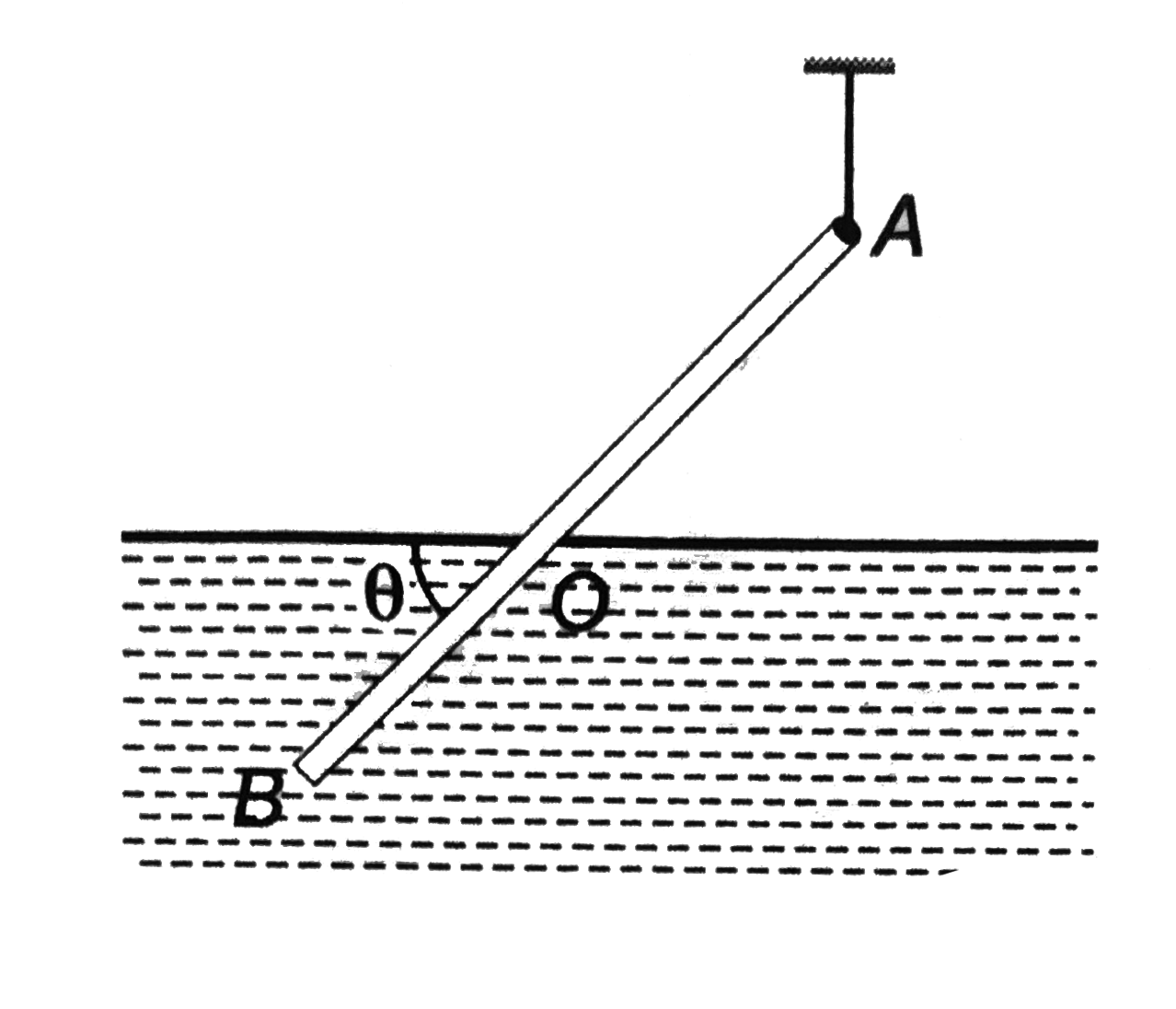
The correct Answer is:A, B, C
T+U=60+w…(i)
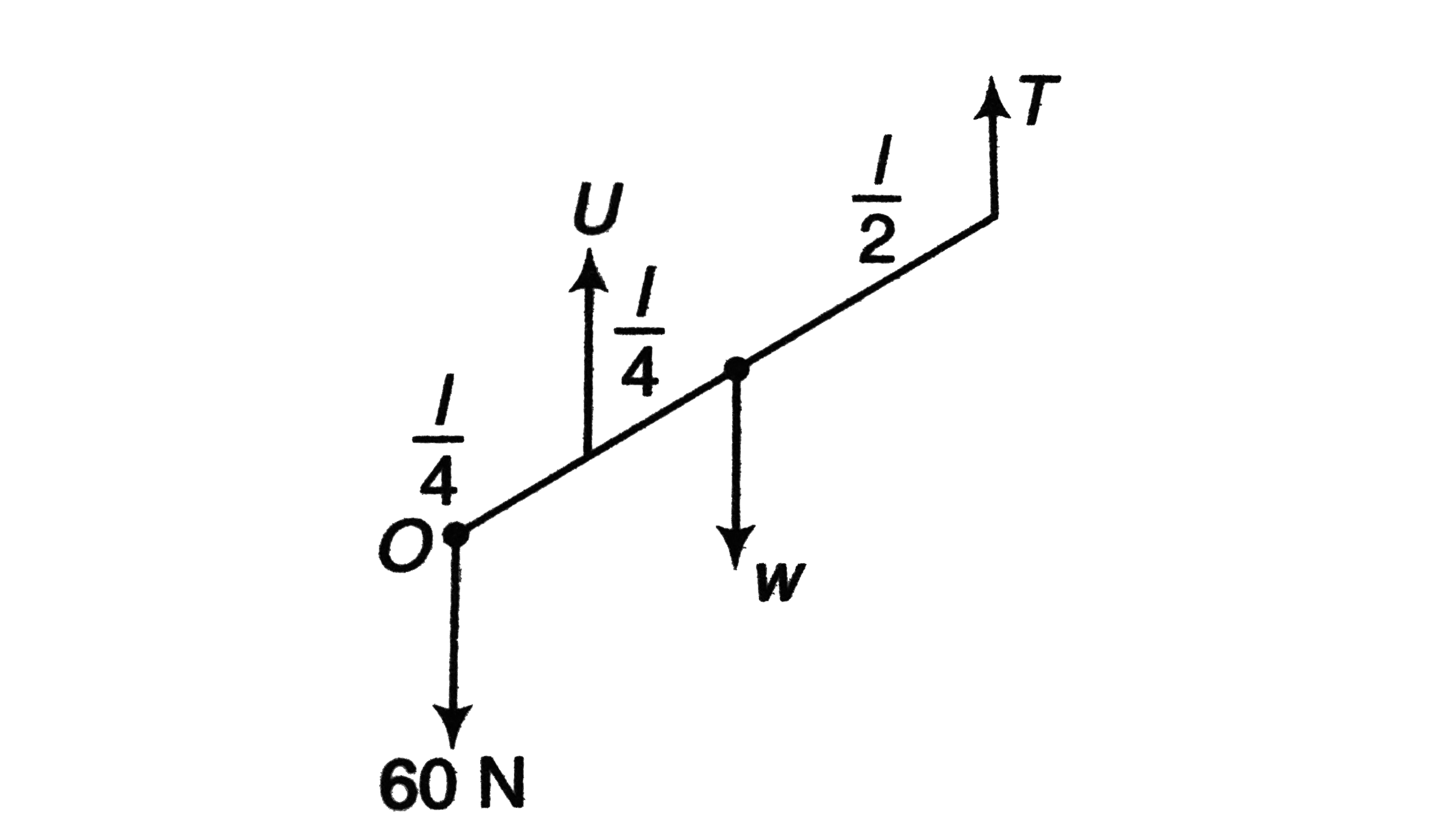
Σ (Moments) about =O
∴=U(l4)+T(l)=W(l2)
or U+4T=2W …(ii)
w=120N….(iii)
Solving these three equations we get T=20n and U=160N
Now, 160(V2)ρwg=(V2)(1000)(10)
∴V=32×10−3m3.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question2videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct36videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct49videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A uniform rod of length L and weight WR is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle θ to the rod. What is the tension T in the wire ?
 View Solution
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View SolutionA uniform rod of weight Fg and length L is supported at its ends by a frictionless through as shown in figure. (a) Show that the centre of gravity of the rod must be vertically over point O when the rod is in equilibrium. (b) Determine the equilibrium value of the angle θ.
 View Solution
View SolutionA light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.
 View Solution
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
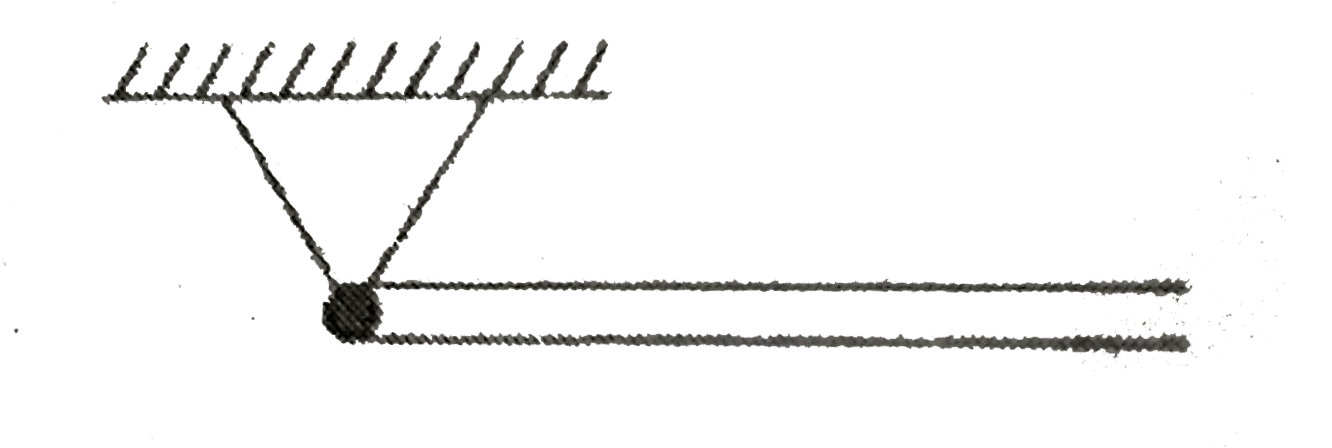 View Solution
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png) View Solution
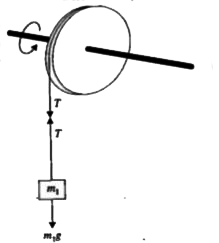
View SolutionA wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
 View Solution
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Vertical component of the force applied by the hinge
Vertical component of the force applied by the hingeView SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.View Solution

