When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time T. When the same body slides down from the rest along a rough inclined plane making the same angle and through the same distance, it takes time aT, where a is a constant greater than 1. The co-efficient of friction between the body and the rough plane is 1√x(a2−1a2) where x = ________.
The correct Answer is:2
To solve the problem, we need to analyze the motion of a body sliding down two different inclined planes: one smooth and one rough. We will derive the expressions for the distance traveled in both scenarios and equate them to find the coefficient of friction.
1. Identify the Forces on the Smooth Inclined Plane:
- The body is sliding down a smooth inclined plane at an angle of 30∘.
- The forces acting on the body are:
- Gravitational force down the incline: Fgravity=mgsin(30∘)=mg⋅12=mg2
- Normal force: N=mgcos(30∘)=mg⋅√32
2. Calculate the Acceleration on the Smooth Plane:
- Using Newton's second law, F=ma:
mgsin(30∘)=ma⟹mg2=ma⟹a=g2
3. Determine the Distance Traveled on the Smooth Plane:
- The body starts from rest, so initial velocity u=0.
- Using the equation of motion s=ut+12at2:
L=0+12⋅g2⋅T2=gT24
4. Identify the Forces on the Rough Inclined Plane:
- The body slides down a rough inclined plane with the same angle of 30∘.
- The forces acting on the body are:
- Gravitational force down the incline: Fgravity=mgsin(30∘)=mg2
- Frictional force: Ffriction=μN=μmgcos(30∘)=μmg⋅√32
5. Calculate the Acceleration on the Rough Plane:
- Applying Newton's second law:
mgsin(30∘)−Ffriction=ma
mg2−μmg⋅√32=ma
- Rearranging gives:
a=g(12−μ⋅√32)
6. Determine the Distance Traveled on the Rough Plane:
- The body takes time aT to slide down the rough plane:
L=12a(aT)2=12g(12−μ⋅√32)(a2T2)
7. Equate the Distances Traveled:
- Since both distances are equal:
gT24=12g(12−μ⋅√32)(a2T2)
- Cancel gT2 from both sides:
14=14−μ⋅√34a2
- Rearranging gives:
μ⋅√3⋅a2=0⟹μ=1−1a2√3
8. Substituting for Coefficient of Friction:
- The coefficient of friction is given as:
μ=a2−1a2√3
- Therefore, we can identify x as:
x=3
Final Answer:
The value of x is 3.
- The body is sliding down a smooth inclined plane at an angle of 30∘.
- The forces acting on the body are:
- Gravitational force down the incline: Fgravity=mgsin(30∘)=mg⋅12=mg2
- Normal force: N=mgcos(30∘)=mg⋅√32
- Using Newton's second law, F=ma:
mgsin(30∘)=ma⟹mg2=ma⟹a=g2
- The body starts from rest, so initial velocity u=0.
- Using the equation of motion s=ut+12at2:
L=0+12⋅g2⋅T2=gT24
- The body slides down a rough inclined plane with the same angle of 30∘.
- The forces acting on the body are:
- Gravitational force down the incline: Fgravity=mgsin(30∘)=mg2
- Frictional force: Ffriction=μN=μmgcos(30∘)=μmg⋅√32
- Applying Newton's second law:
mgsin(30∘)−Ffriction=ma
mg2−μmg⋅√32=ma
- Rearranging gives:
a=g(12−μ⋅√32)
- The body takes time aT to slide down the rough plane:
L=12a(aT)2=12g(12−μ⋅√32)(a2T2)
- Since both distances are equal:
gT24=12g(12−μ⋅√32)(a2T2)
- Cancel gT2 from both sides:
14=14−μ⋅√34a2
- Rearranging gives:
μ⋅√3⋅a2=0⟹μ=1−1a2√3
- The coefficient of friction is given as:
μ=a2−1a2√3
- Therefore, we can identify x as:
x=3
The value of x is 3.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A)
81 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section A
39 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
 .
.
View SolutionDerive an expression for the work done when a body slides down a rough inclined plane.
View Solution
Knowledge Check
When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p is, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
Aμ=(1−1p2)1√3Bμ=(1−19p2)Cμ=(1−p2)1√3Dμ=√1−9p2When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
 .A(1−1P2)B(1+1P2)C1P2D−1P2
.A(1−1P2)B(1+1P2)C1P2D−1P2A body of mass m is launched up on a rough inclined plane making an angle 45∘ with horizontal If the time of descent between plane and body is
A25B35C34D45
Starting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ. It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by:-
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizantal. If the coefficient of friction is0.3 then acceleration of the body is
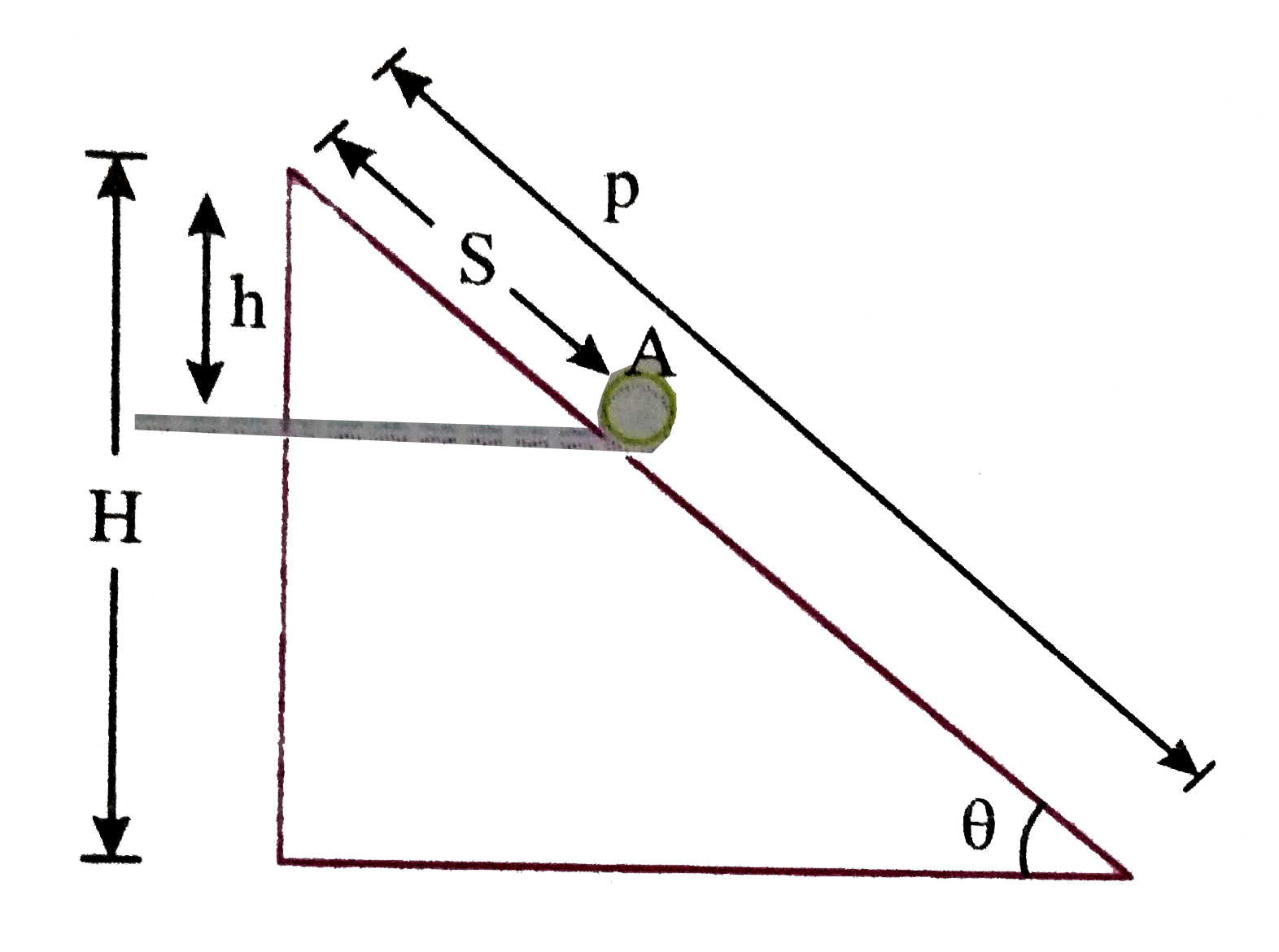
View SolutionA particle sides down from rest on an inclined plane of angle θ with horizontal. The distances are as shown. The particle slides down to the position A, where it velocity is v.
 .
.
View Solution
