When a coil joined to a cell, the current through the coil grows with a time constant τ. After what time, the current will reach 10% of its steady- state value?
To solve the problem of determining the time at which the current through a coil reaches 10% of its steady-state value, we can follow these steps:
Step 1: Understand the steady-state current
Let I0 be the steady-state current value. We want to find the time t when the current I reaches 10% of I0. Therefore, we can express this as:
I=0.1I0
Step 2: Use the formula for current growth in an LR circuit
The current I through an inductor in an LR circuit as a function of time t is given by:
I(t)=I0(1−e−tτ)
where τ is the time constant.
Step 3: Set up the equation
Substituting I=0.1I0 into the growth equation gives:
0.1I0=I0(1−e−tτ)
Step 4: Simplify the equation
Dividing both sides by I0 (assuming I0≠0):
0.1=1−e−tτ
Step 5: Rearrange to isolate the exponential term
Rearranging the equation gives:
e−tτ=1−0.1=0.9
Step 6: Take the natural logarithm
To solve for t, take the natural logarithm of both sides:
−tτ=ln(0.9)
Step 7: Solve for t
Multiplying both sides by −τ gives:
t=−τln(0.9)
Final Result
Thus, the time t at which the current reaches 10% of its steady-state value is:
t=−τln(0.9)
Let I0 be the steady-state current value. We want to find the time t when the current I reaches 10% of I0. Therefore, we can express this as:
I=0.1I0
The current I through an inductor in an LR circuit as a function of time t is given by:
I(t)=I0(1−e−tτ)
where τ is the time constant.
Substituting I=0.1I0 into the growth equation gives:
0.1I0=I0(1−e−tτ)
Dividing both sides by I0 (assuming I0≠0):
0.1=1−e−tτ
Rearranging the equation gives:
e−tτ=1−0.1=0.9
To solve for t, take the natural logarithm of both sides:
−tτ=ln(0.9)
Multiplying both sides by −τ gives:
t=−τln(0.9)
Thus, the time t at which the current reaches 10% of its steady-state value is:
t=−τln(0.9)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA58videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
Two different coils have self-inductances L1=8mHandL2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are i1,V1andW1 respectively. Corresponding values for the second coil at the same instant are i2,V2andW2 respectively. Then:
AW2W1=8BW2W1=18CW2W1=4DW2W1=14
A coil of self-inductance 50 henry is joined to the terminals of a battery of e.m.f. 2 volts through a resistance of 10ohm and a steady current is flowing through the circuit. If the battery is now disconnected, the time in which the current will decay to 1/e of its steady value is
View SolutionA coil of inductance 300mh and resistance 2Ω is connected to a source of voltage 2V. The current reaches half of its steady state value in
View SolutionA circuit consists of a coil, a switch and a battery, all in series. The internal resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
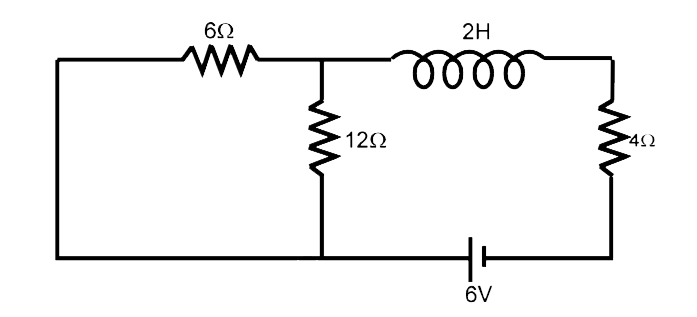
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value? a)20% b) 8% c) 4% d)10 %View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then the current through the battery steady state reached is
 View Solution
View SolutionTwo different coils have self inductances L1=9mH and L2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coils is the same. At that time, the current the induced voltage and the energy stored in the first coil are i1,V1 and W1 respectively.
Corresponding values for the second coil at the same instant are i2,V−2 and W2 respectively. Then,View SolutionA coil has an inductance of 50mH and a resistance of 0.3Ω. If a 12V emf is applied across the coil, the energy stored in the magnetic field after the current has built up of its steady state value is
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View Solution