When a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths and , and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring.
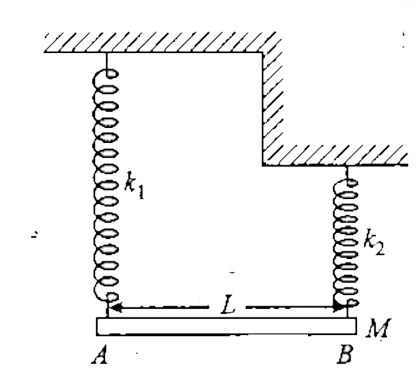
Step by step video & image solution for When a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths l//3 and 2l//3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exerice 2.1
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exerice
4 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
When a 1.0kg mass hangs attached to a spring of length 50cm, the spring stretches by 2cm. The mass is pulled down until the length of the spring becomes 60cm. What is the amount of elastic energy stored in the spring in this condition. if g=10m/s2.
View SolutionA simple spring has length l and force constant K. It is cut into two springs of lengths l1andl2 such that l1=nl2 (n = an integer). The force constant of spring of length l1 is
View Solution
Knowledge Check
A spring of constant K is cut into two parts of length in the ratio 2:3 . The spring constant of large spring is
A53KB23KCkD35kA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
Al2l1B2l2l1Cl1l2DNoneA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
Amg(l+y)B12mg(l+y)C12mgyDMgy
A mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
View SolutionIf a spring of stiffness 'k' is cut into two parts 'A' and 'B' of length lA:lB=2:3, then the stiffness of spring 'A' is given by
View SolutionA spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
View SolutionTwo identical springs are connected to mass m as shown (k = spring constant). If the period of the configuration (i) is 2 s, the period of the configuration (ii) is
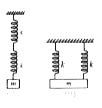
View SolutionA spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
View Solution
