When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0) (see figure).
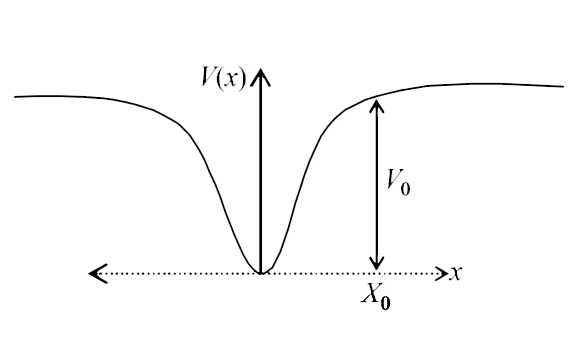 .
.
For periodic motion of small amplitude A,the time period (T) of thes particle is proportional to.
A
(a) Asqrtm/a
B
(b) 1/Asqrtm/a
C
(c ) Asqrta/m
D
(d) 1A√am.
Video Solution
Text Solution
The correct Answer is:B
(b) We can get the answer of this question with the help of dimensional analysis.
Given potential energy =ax4
aPotentiale≠rgyx4=(ML2T−2)L4=[Ml−2t−2].<br>Now1A√ma=1Lsq−2T−2)=T
Therefore potion (b) is correct.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
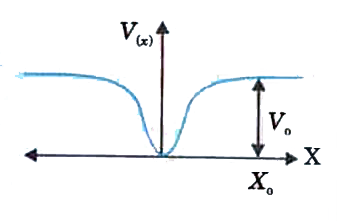
For periodic motion os small amplitude A . The time periodic T of this particle is proportional toAA√mαB1A√mαCA√αmD1A√αmWhen a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0

The acceleration of this particle for |X|>X0 isAproportional to (v0mX0)Bpropotinal to √V0mX0Cproportional to V0DZeroWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=α⋅x4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
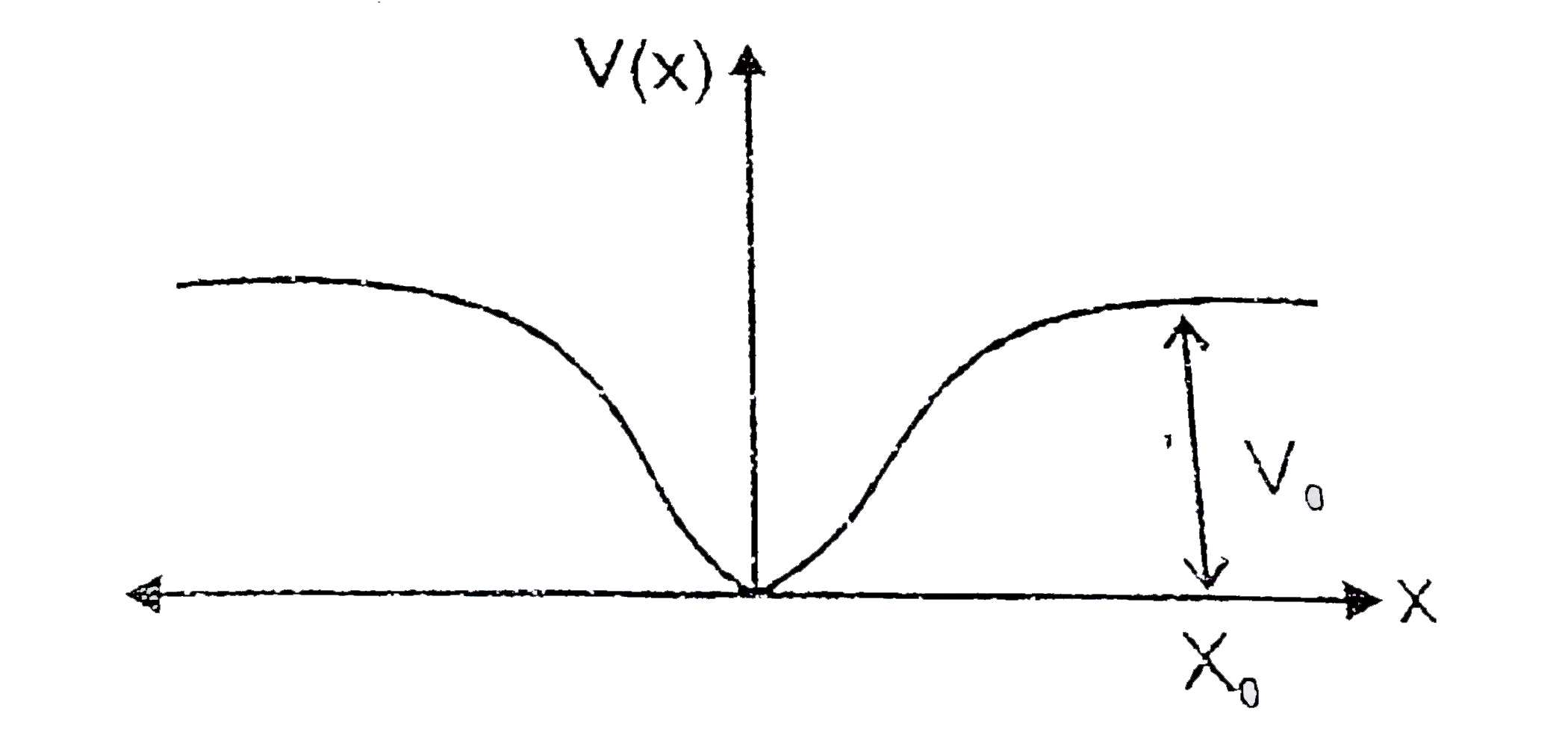
If the total energy of the particle is E, it will perform is periodic motion why if :AE<0BE>0CV0>E>0DE>V0
Apaticle of mass m moves in the potential energy U shown above. Find the period of the motion when the particle has total energy E.
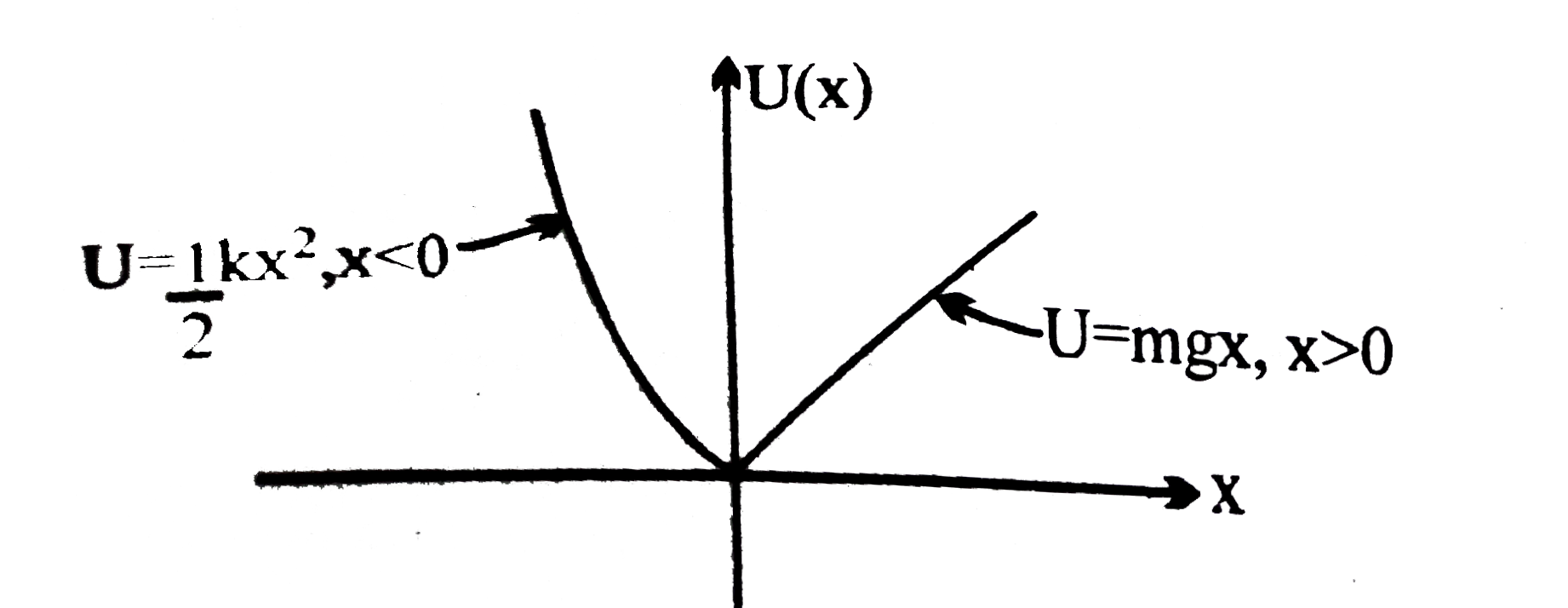
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionA particle is executing simple harmonic motion .Its total energy is proportional to its -
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionA particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View Solution
