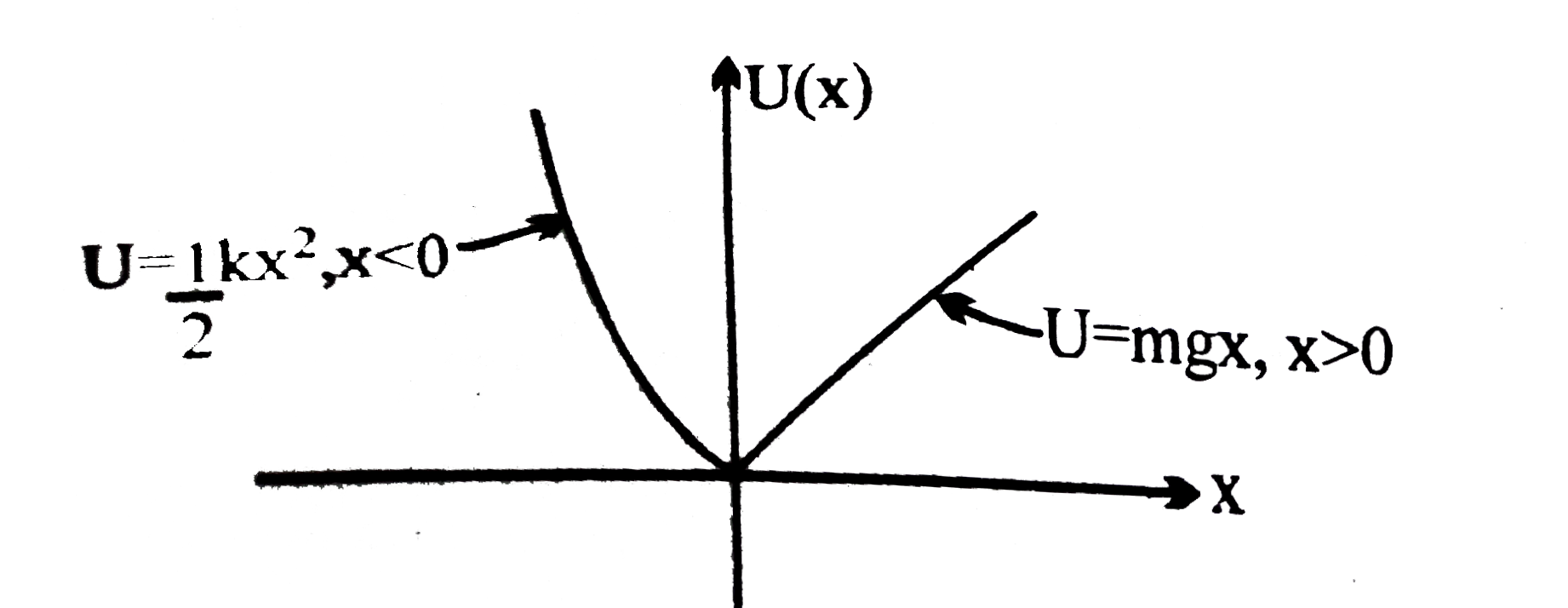
A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
2π√mk+4√2Emg2
2π√mk
π√mk+2√2Emg2
2√2Emg2
The correct Answer is:C
To find the period of motion for a particle of mass m moving in a potential energy curve with total energy E, we can break down the solution into several steps.
Step 1: Analyze the Potential Energy Curve
The potential energy U is given as:
- For the left side: U=12kx2 (which represents a harmonic oscillator)
- For the right side: U=mgx (which represents a linear potential)
Step 2: Determine the Motion on the Left Side
For the left side of the curve:
- The force F can be derived from the potential energy:
F=−dUdx=−ddx(12kx2)=−kx
- This indicates that the motion is simple harmonic motion (SHM) with:
a=−kmx
- The angular frequency ω is given by:
ω=√km
- The time period T for a complete oscillation in SHM is:
T=2π√mk
Step 3: Calculate the Time for Left Side Motion
Since the particle moves from the mean position to the extreme position and back to the mean position, the time taken for this half cycle (left side) is:
Tleft=T2=π√mk
Step 4: Determine the Motion on the Right Side
For the right side of the curve:
- The force F is:
F=−mg
- The particle will accelerate downwards under gravity until it reaches the maximum displacement where its kinetic energy is zero.
Step 5: Calculate the Maximum Velocity
At the lowest point (where potential energy is minimum), the kinetic energy is equal to the total energy E:
12mv2=E⟹v=√2Em
Step 6: Calculate Time to Stop
Using the equation of motion:
v=u−gt
Setting v=0 (when the particle stops), we have:
0=√2Em−gt⟹t=√2Emg=1g√2Em
This is the time taken to stop, denoted as t.
Step 7: Calculate Total Time for Right Side Motion
The time to go down and come back to the origin is:
Tright=2t=2(1g√2Em)=2g√2Em
Step 8: Calculate Total Period of Motion
The total period Ttotal is the sum of the left and right side times:
Ttotal=Tleft+Tright=π√mk+2g√2Em
Final Expression
Thus, the period of the motion when the particle has total energy E is:
T=π√mk+2g√2Em
The potential energy U is given as:
- For the left side: U=12kx2 (which represents a harmonic oscillator)
- For the right side: U=mgx (which represents a linear potential)
For the left side of the curve:
- The force F can be derived from the potential energy:
F=−dUdx=−ddx(12kx2)=−kx
- This indicates that the motion is simple harmonic motion (SHM) with:
a=−kmx
- The angular frequency ω is given by:
ω=√km
- The time period T for a complete oscillation in SHM is:
T=2π√mk
Since the particle moves from the mean position to the extreme position and back to the mean position, the time taken for this half cycle (left side) is:
Tleft=T2=π√mk
For the right side of the curve:
- The force F is:
F=−mg
- The particle will accelerate downwards under gravity until it reaches the maximum displacement where its kinetic energy is zero.
At the lowest point (where potential energy is minimum), the kinetic energy is equal to the total energy E:
12mv2=E⟹v=√2Em
Using the equation of motion:
v=u−gt
Setting v=0 (when the particle stops), we have:
0=√2Em−gt⟹t=√2Emg=1g√2Em
This is the time taken to stop, denoted as t.
The time to go down and come back to the origin is:
Tright=2t=2(1g√2Em)=2g√2Em
The total period Ttotal is the sum of the left and right side times:
Ttotal=Tleft+Tright=π√mk+2g√2Em
Thus, the period of the motion when the particle has total energy E is:
T=π√mk+2g√2Em
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Apaticle of mass m moves in the potential energy U shown above. Find the period of the motion when the particle has total energy E.
 View Solution
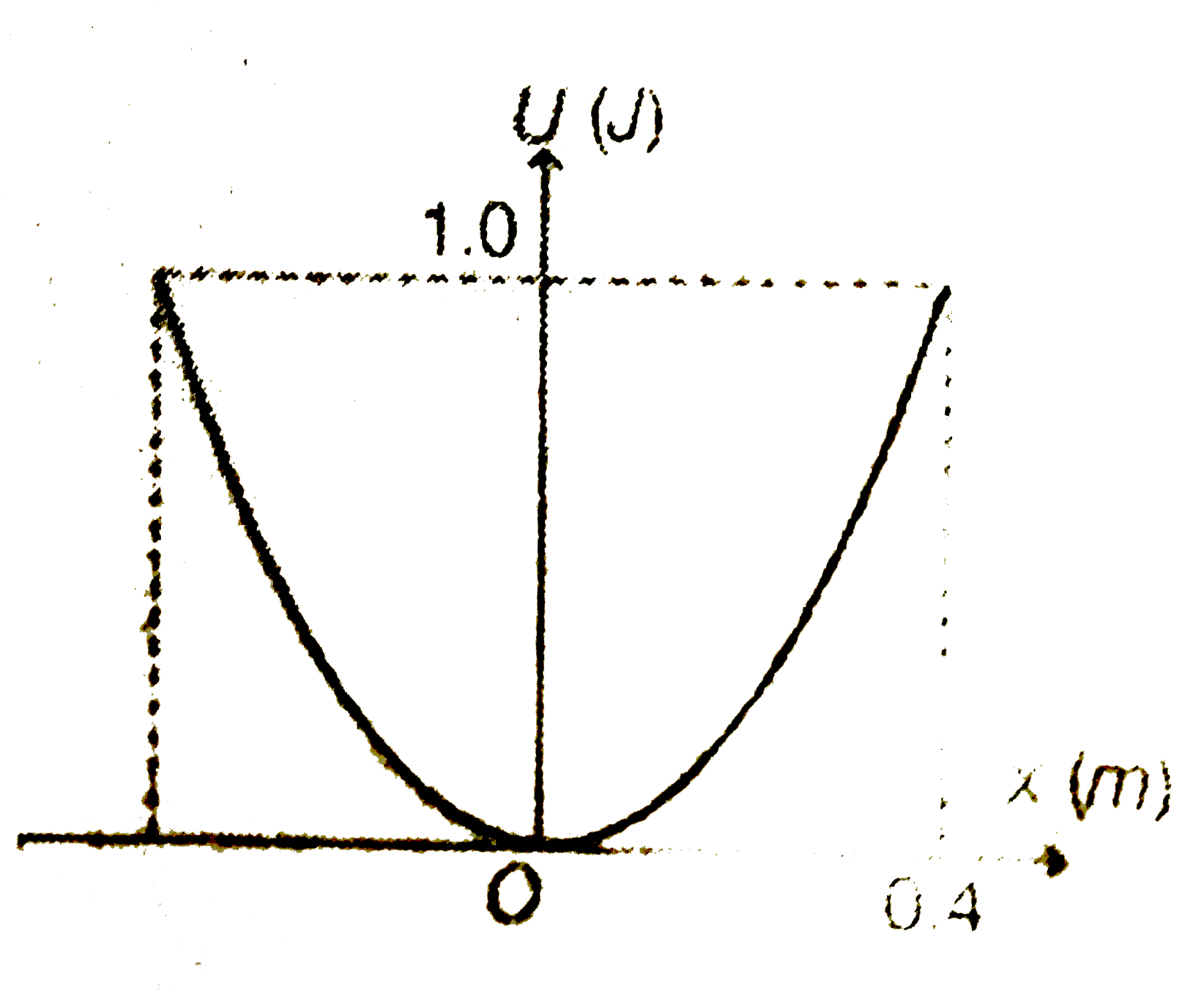
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
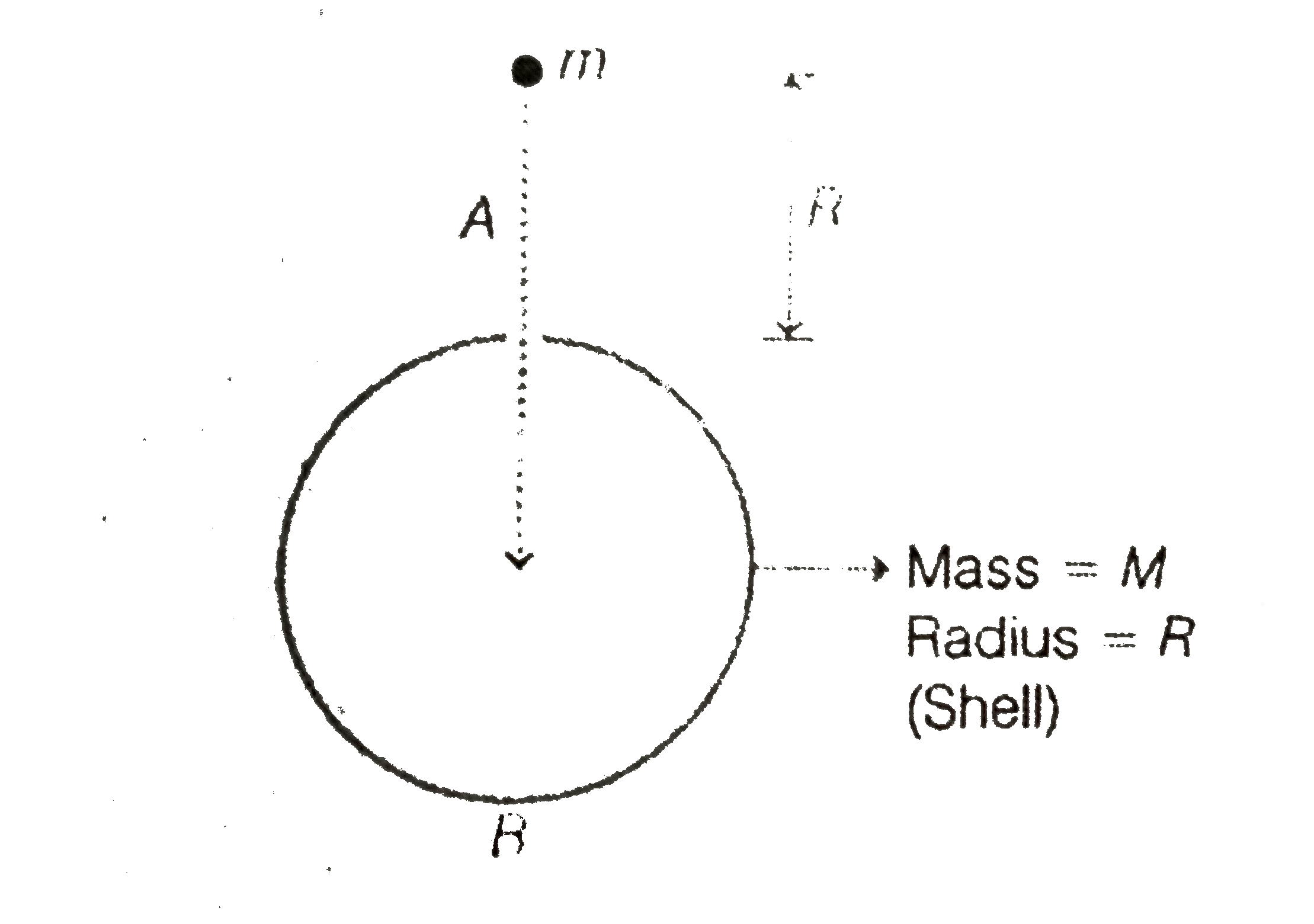
A particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
 Awill continuously increasesBwill continuously decreasesCwill first increase and then become constantDwill first decreases and then become constant
Awill continuously increasesBwill continuously decreasesCwill first increase and then become constantDwill first decreases and then become constant - Question 2 - Select One
A particle of mass m moving with kinetic energy K, makes a head - on elastic collision with a stationary particle of mass ηm. The maximum potential energy stored in the system during the collision is
Aηη+1KBη+1ηKC(η−1)KD(η−1)K - Question 3 - Select One
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 A2π5sB2√2π5sC√2π5sD4π5s
A2π5sB2√2π5sC√2π5sD4π5s
A particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form u(x) = ax2−bx), where a and b are positive constants. Find the period of small oscillations of the particle.
View SolutionA small particle of mass m, moves in such a way that the potential energy U=ar3, where a is position constant and r is the distance of the particle from the origin. Assuming Rutherford's model of circular orbits, then relation between K.E and P.E of the particle is :
View SolutionA particle of mass m when annihilated completely gives energy E equal to
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form U(x)=ax2−bx where a and b are positive constants. The position of equilibrium is:
View SolutionA particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
View Solution

