When a piece of wood is suspended from the hook of a spring balance, it reads 70 gf. The wood is now lowered into water. What reading do you expect on the scale of spring balance?
To solve the problem step by step, we will analyze the situation of the piece of wood being suspended in air and then submerged in water.
1. Identify the weight of the wood in air:
The spring balance reads 70 gf when the wood is suspended in air. This means the weight of the wood in air is 70 gf.
2. Understand the concept of buoyancy:
When an object is submerged in a fluid (in this case, water), it experiences an upward force known as buoyancy or upthrust. This force is equal to the weight of the fluid displaced by the object.
3. Determine if the wood will float:
Since wood is less dense than water, it will float when placed in water. This means that the weight of the wood will be balanced by the buoyant force acting on it.
4. Calculate the apparent weight when submerged:
The apparent weight of the wood when submerged in water can be calculated using the formula:
Apparent Weight=Weight of Wood in Air−Upthrust
Since the wood is floating, the upthrust is equal to the weight of the wood in air, which is 70 gf.
5. Substituting the values:
Apparent Weight=70 gf−70 gf=0 gf
6. Conclusion:
When the wood is submerged in water, the reading on the spring balance will be 0 gf because the buoyant force completely counteracts the weight of the wood.
Final Answer:
The reading on the scale of the spring balance when the wood is submerged in water will be 0 gf.
The spring balance reads 70 gf when the wood is suspended in air. This means the weight of the wood in air is 70 gf.
When an object is submerged in a fluid (in this case, water), it experiences an upward force known as buoyancy or upthrust. This force is equal to the weight of the fluid displaced by the object.
Since wood is less dense than water, it will float when placed in water. This means that the weight of the wood will be balanced by the buoyant force acting on it.
The apparent weight of the wood when submerged in water can be calculated using the formula:
Apparent Weight=Weight of Wood in Air−Upthrust
Since the wood is floating, the upthrust is equal to the weight of the wood in air, which is 70 gf.
Apparent Weight=70 gf−70 gf=0 gf
When the wood is submerged in water, the reading on the spring balance will be 0 gf because the buoyant force completely counteracts the weight of the wood.
The reading on the scale of the spring balance when the wood is submerged in water will be 0 gf.
Topper's Solved these Questions
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (3 Marks Questions )
23 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (4 Marks Questions )
16 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (4 Marks Questions )
10 Videos
- ELECTRICITY AND MAGNETISM BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )
6 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
Similar Questions
a metal solid cylinder tied ot a thread is hanging from the hook of a spring balance. The cylinder is gradually immersed into water contaned in a jar. What changes do you expect in the readings of spring balance? Explain your answer.
View SolutionThe reading in the spring balance is

View SolutionThe reading in the spring balance is:

View SolutionA cubical block (side l) is in equilibrium at the interface of two liquids A and B. The spring balance reads W Newton. If the block is weighted in air, the reading of the spring balance will be :

View SolutionAn object is suspended from a spring balance in a lift. The reading is 240 N when the lift is at rest. If the spring balance reading now change to 220N, then the lift is moving
View SolutionFor the arrangement shown in the figure, the reading of spring balance is

View SolutionA wooden block of volume 1000cm3 is suspended from a spring balance its weight is 12 N in air. It is suspended in water such that half of the block is below the surface of water. The reading of spring balance is
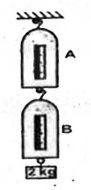
View SolutionA block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
View SolutionA block of mass 20 kg is suspended through two light spring balances as shown in fig. Calculate the:

(a) reading of spring balance (1),
(b) reading of spring balance (2).
View Solution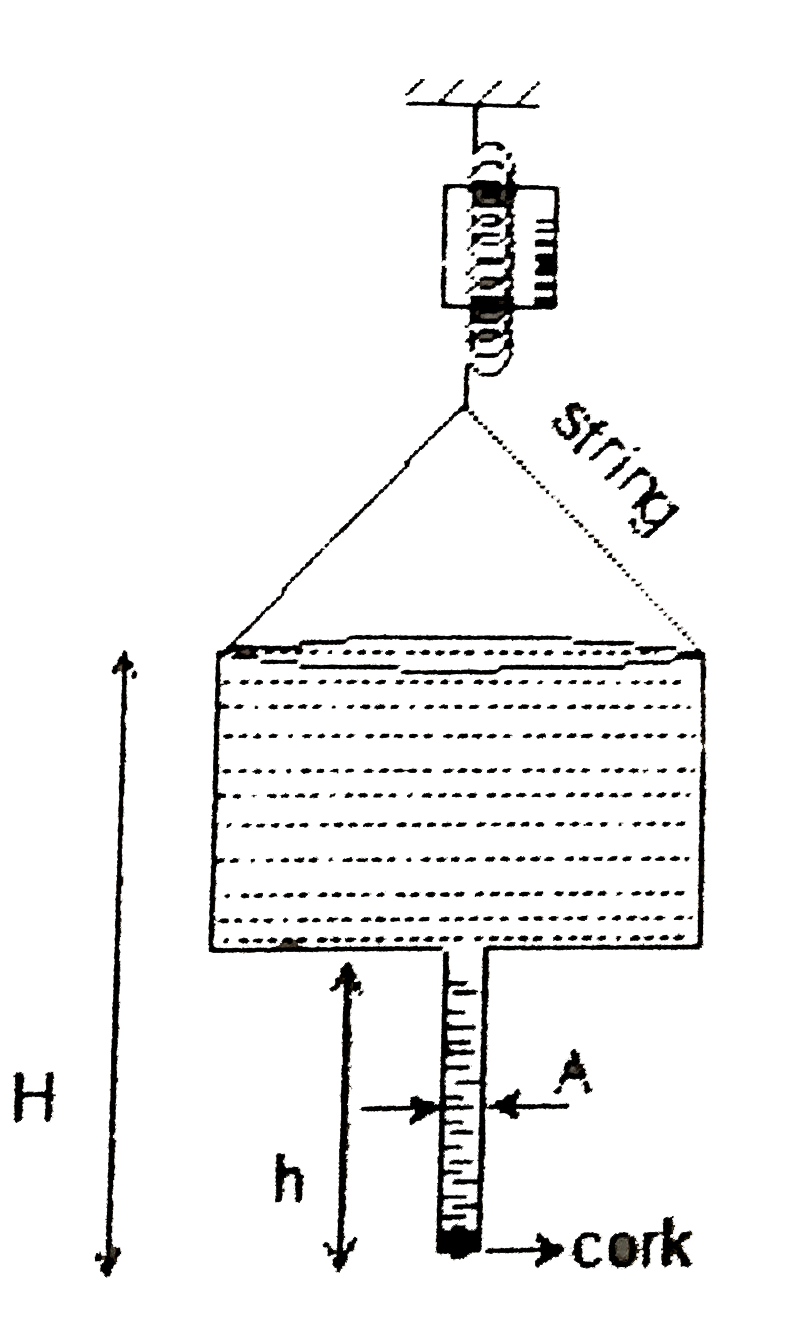
A vessel completely filled wit water is suspended with help of strings from a spring balance as shwon in figure. A cork is plugged at the bottom of the vessel. If the initial reading of the spring balannce is W0. Then the reading of the spring balance just after the cork is removed and the liquid begins to flow out will be [ρ= density of liquid & A=coss -sectional area of narrow pipe]
View Solution
