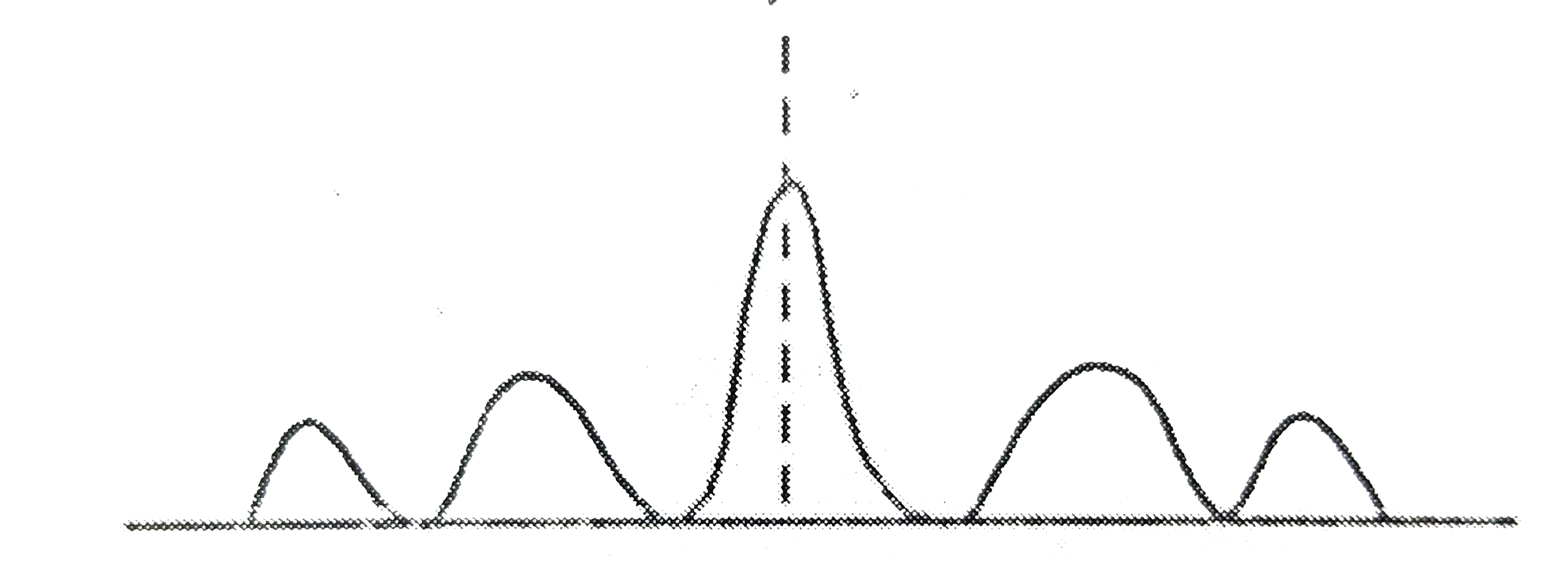
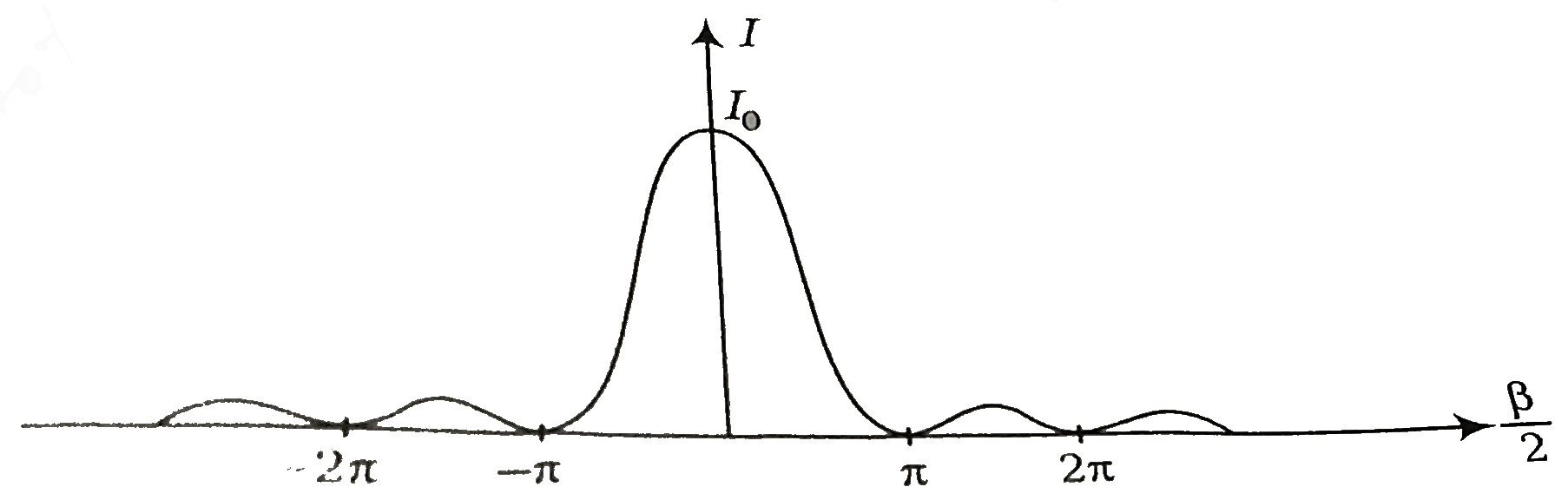
When a plane wave front of light, of wavelength $λ$ , is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.

(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?

Text Solution

Verified by Experts

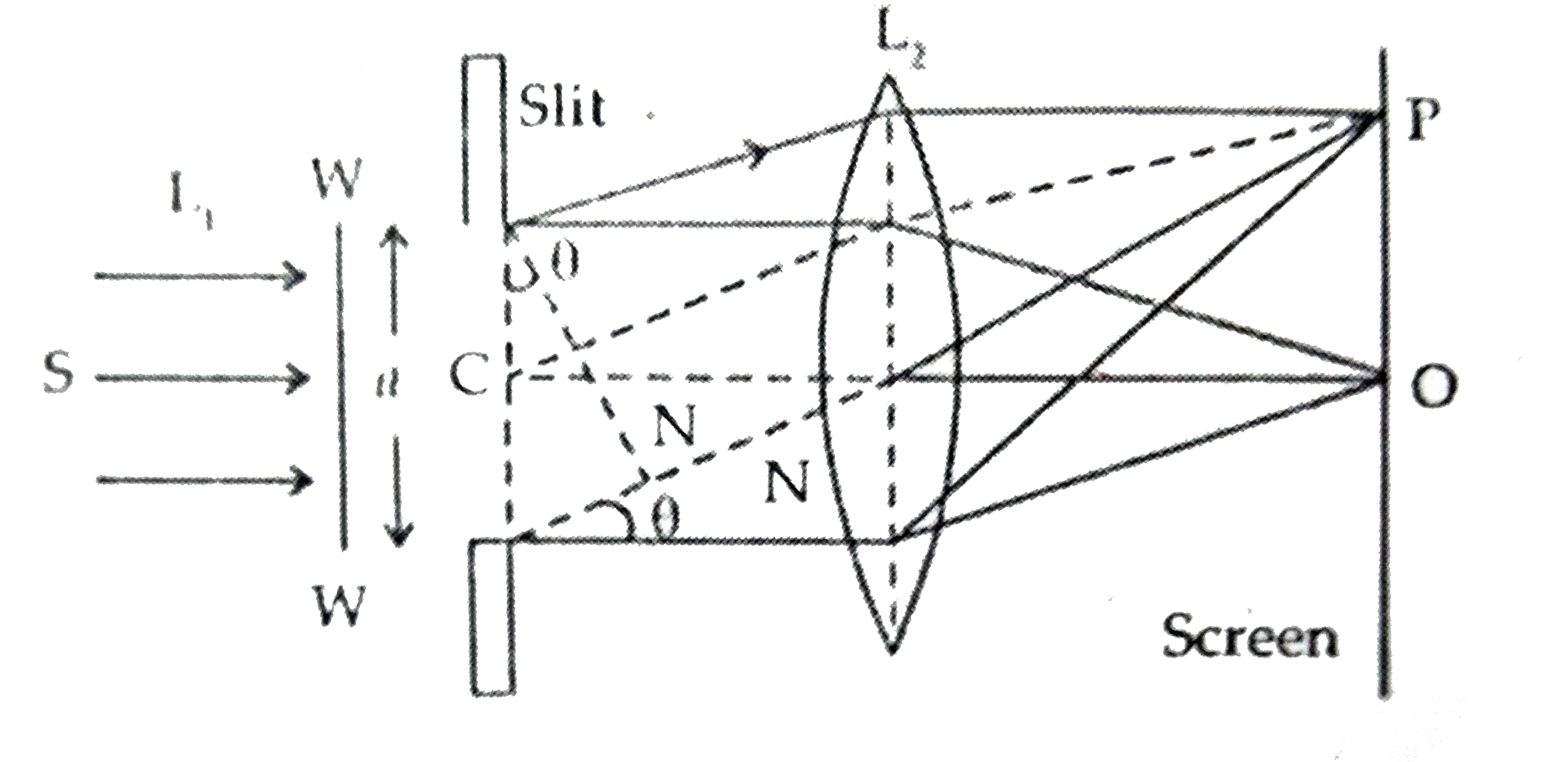
Phenomenon is Diffraction. All the secondary wavelets going straight across the slit are focussed at the central point of the screen. The wavelets from any two corresponding points of the two halves of the slit reach the point O in the same phase, they add constructively to produce a central bright fringe. The condition for first dark fringe is
$a {sin θ}_{1} = λ$
Similarly, the condition for second dark fringe will be
$a {sin θ}_{2} = 2 λ$
Hence, the condition for n th dark fringe can be written as
$a {sin θ}_{n} = n λ, n = 1, 2, 3, ...$
The directions of various minima are given by
$θ_{n} \approx {sin θ}_{n} = n \frac{λ}{a} [As λ < < a, so {sin θ}_{n} = θ_{n}]$
Suppose the point P is so located that $p = \frac{3 λ}{2}$
When $θ = θ_{1}$ , then a ${sin θ}_{1} = \frac{3}{2} λ$
We can divide the slit into three equal parts. The path difference between two corresponding points of the first two parts will be $\frac{λ}{2}$ . The wavelets from these points will interfere destructively. However, the wavelets from the third part of the slit will contribute to some intensity forming a secondary maximum. The intensity of this maximum is much less than that of the central maximum.
Thus, the condition for the first secondary maximum is
$s {sin θ}_{1}' = \frac{3}{2} λ$ .
Similarly, the condition for the second secondary maximum is
$a {sin θ}_{2}' \frac{5}{2} λ$ .
Hence the condition for nth secondary maximum can be written as
$a {sin θ}_{n}' = (2 n + 1) \frac{λ}{2}, n = 1, 2, 3 ... ... .$
The directions of secondary maxima are given by
$θ_{n}' \approx θ_{n}' (2 n +_{1}) \frac{λ}{2 a}$ .

Updated on:21/07/2023