When a solid moves therough a liquid, the liquid opposes the miotioon with a force F. The magnitude of F depends on the coefficient of viscosity $η$ of the liquid, the radius r of the sphere aknd the speed v of the sphere. Assuming that F is proportional to different powers of these quantities, guess a formula for F using the method of dimension.

Video Solution

Text Solution

Verified by Experts

Suppose the formula is $F = k η^{a} r^{b} v^{c}$ .
Then, $M L T^{- 2} = {[M L^{- 1} T^{- 1}]}^{a} L^{b} {(\frac{L}{T})}^{c}$
$= M^{a} L^{- (a + b + c)} T^{- a - c}$
Equating the exponents of M,L and T from both sides, $$ a=1 $$ -a+b+c=1 $$ -a-c=-2 $ S o l v \in g t h e s e$ a=, b=1, and c=1. $ s o l v \in g t h e s e$ a=1, b=1, and c=1 $. T h u s, t h e f or μ l a f or$ f is $F = K η r v$ .

Updated on:21/07/2023

A small metal sphere of radius a is falling with a velocity $υ$ through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is $η$ , then the sphere encounters an opposing force of
A $6 π η a^{2} υ$
B $\frac{6 η υ}{π a}$
C $6 π η a υ$
D $\frac{π η υ}{6 a^{3}}$
A liquid of coefficient of viscosity $η$ is flowing steadily through a capillary tube of radius r and length I. If V is volume of liquid flowing per sec. the pressure difference P at the end of tube is given by
A $P = \frac{8 π I V}{η r^{4}}$
B $P = \frac{8 η r^{4} I}{π V}$
C $P = \frac{8 η I V}{π r^{4}}$
D $P = \frac{8 η r^{4} V}{π I}$
A solid sphere of mass m, suspended through a string in a liquid as shown. The string has some tension Magnitudes of net force due to liquid on upper hemisphere and that on lower hemisphere are $F_{A}$ and $F_{B}$ respectively. Which of the following is // are true.

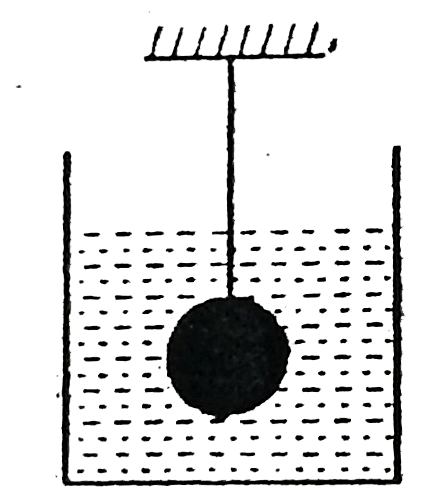ADensity of material of the sphere is greater than density of liquid
BDifference of $F_{B}$ and $F_{A}$ is dependent of atmoshperic pressure
C $F_{B} - F_{A} = m g$
D $F_{B} - F_{A} < m g$