When air of density 1.3kg/m3 flows across the top of the tube shown in the accompanying figure, water rises in the tube to a height of 1.0cm. What is the speed of air?

The correct Answer is:A, B, D
12ρairv2=ρwghw
v=√2ρwghwρair
√2×103×10×10−21.3
=12.4m/s.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct
49 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A light cylindrical tube 'T' of length l and radius 'r' containing air is inverted in water (density d). One end of the tube is open and the other is closed A block 'B' of density 2d is kept on the tube as shown in the figure. The tube stays in equilibrium in the position shown. (Assume the atmosphere pressure is to be P0)
Assume that density of air is very small than density of block and water. Pick up the correct statement (s)

View SolutionA narrow tube 50 cm length is closed at one end contains air trapped by a certain column of Hg. When the tubes is held horizontally, the air column in if has a length of 10cm. What is the pressure exerted by air when the tube is held vertically with the open end at the bottom and the length of the air column is 15cm? Also find the vertical height of the mercury column inside the tube.
View SolutionA capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View SolutionAt the middle of the mercury barometer tube there is a little column of air with the length l0 and there is vacuum at the top as shown. Under the normal atmospheric pressure and the temperature of 200 le,vom/ l0=10cm. What will be the length of the air column if the temperature rises to 330 kelvin? (Neglict expansion of the tube)
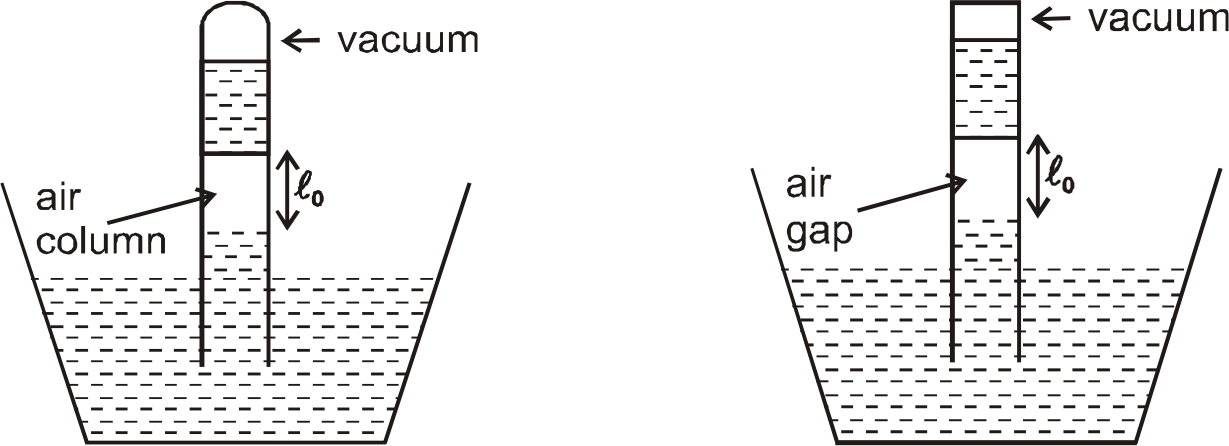
View SolutionWater rises to a height of 16.3 cm in a capillary of height 18 cm above the water leve. If the tube is cut at a height of 12 cm -
View SolutionA tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water , figure. The water level in the tube is gradually lowerd. When the water level is 17cm below the open end, maximum intensity of sound in heard. If the room temperature is 20∘C, calculate
(a) speed of sound in air at room temperature.
(b) speed of sound in air at 0∘C
(c) if the water in the tube is replaced with mercury, will there be any difference in your observations?

View SolutionThe figure shows a crude type of perfume atomizer. When bulb at A is compressed, air flows swifty through the tiny BC with uniform speed v, there by causing a reduced pressure at the position of verticall tube DE. The liquid of density 500kg/m3, then rises in the tube, enters tube BC and sprayed out. When bulb is in natural position the air in the bulb and tube are at atmospheric pressure P50=15N/m2. When bulb A is compressed, it creates an exces pressure Δp=0.001P0 inside the bulb A. Density of air is 1.3kg/m3. If the magnitude of minimum value of speed v required to cause the liquid to rise to tube BC is 5km/s. Find the value of k. (g=10m/s2)

View SolutionA rain drop with radus 1.5 mm falls from a cloud at a height 1200 m from ground . The density of water is 1000 kg/m3 and density of air is 1.2kg/m3. Assume the drop was spherical throughout the fall and there is no air drag. The impact speed of the drop will be :
View SolutionFigure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View Solution
