When an ideal gas in a cylinder was compreswsed isothermally by a piston, the work done on the gas found to be 1.5×104 cal. During this process about
The correct Answer is:3.6×103
To solve the problem, we need to analyze the isothermal compression of an ideal gas and understand the relationship between work done, heat transfer, and internal energy.
1. Understanding Isothermal Process:
In an isothermal process, the temperature of the gas remains constant. For an ideal gas, this means that the internal energy (U) does not change, i.e., ΔU=0.
2. Work Done on the Gas:
The work done on the gas during isothermal compression is given as W=1.5×104 joules.
3. First Law of Thermodynamics:
According to the first law of thermodynamics:
ΔQ=ΔU+W
Since ΔU=0 for an isothermal process, we can simplify this to:
ΔQ=W
4. Substituting the Values:
We substitute the value of work done into the equation:
ΔQ=1.5×104 J
5. Converting Joules to Calories:
To convert joules to calories, we use the conversion factor 1 cal=4.184 J:
ΔQ=1.5×104 J4.184 J/cal≈3580.65 cal
6. Considering Heat Flow Direction:
Since the work is done on the gas, the gas loses heat to the surroundings. Therefore, the heat transfer ΔQ will be negative:
ΔQ≈−3580.65 cal
7. Final Result:
Thus, the amount of heat that flowed out of the gas during the isothermal compression is approximately −3.58×103 cal.
Conclusion:
The correct option, based on the calculations, is that approximately 3.6×103 calories of heat flowed out from the gas.
In an isothermal process, the temperature of the gas remains constant. For an ideal gas, this means that the internal energy (U) does not change, i.e., ΔU=0.
The work done on the gas during isothermal compression is given as W=1.5×104 joules.
According to the first law of thermodynamics:
ΔQ=ΔU+W
Since ΔU=0 for an isothermal process, we can simplify this to:
ΔQ=W
We substitute the value of work done into the equation:
ΔQ=1.5×104 J
To convert joules to calories, we use the conversion factor 1 cal=4.184 J:
ΔQ=1.5×104 J4.184 J/cal≈3580.65 cal
Since the work is done on the gas, the gas loses heat to the surroundings. Therefore, the heat transfer ΔQ will be negative:
ΔQ≈−3580.65 cal
Thus, the amount of heat that flowed out of the gas during the isothermal compression is approximately −3.58×103 cal.
The correct option, based on the calculations, is that approximately 3.6×103 calories of heat flowed out from the gas.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 20
1 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 21
1 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 18
1 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
Similar Questions
Knowledge Check
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)
An ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process

View SolutionAn ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?

View SolutionAssertion : For an isothermal process in an ideal gas, the heat obsorbed by the gas is entirely used in the work done by the gas.
Reason : During a process taking place in a system, the temperature remains constant then the process is isothermal.
View SolutionWork done on an ideal gas in a cylinder when it is compressed by and external pressure in a single step is shown below :

Which of the following graphs will show the work done on the gas ?
View SolutionIn figure, P−V curve of an ideal gas is given. During the process, the cumulative work done by the gas
View Solution5 mole of an ideal gas of volume is expanded against vaccum to make its volume 2 times, then work done by the gas is:
View SolutionAn ideal gas is taken around the cycle ABCA as shown in the P-V diagram. The total work done by the gas during the cycle is
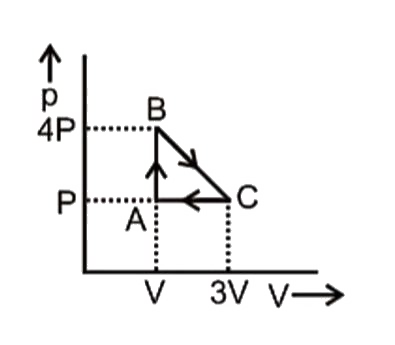
View Solution
