When L and C are in series, voltage across them is in phase (True/false). The current in them is in phase (true/false).
To solve the question, we need to analyze the behavior of an inductor (L) and a capacitor (C) when they are connected in series in an AC circuit. We will evaluate two statements: whether the voltage across them is in phase and whether the current in them is in phase.
1. Understanding Series Connection:
- In a series circuit, the same current flows through all components. Therefore, the current through the inductor (L) and the capacitor (C) is the same.
2. Phase Relationship for Inductor:
- For an inductor, the voltage (V_L) leads the current (I) by a phase angle of π2 (or 90 degrees). This means that if the current is at its maximum, the voltage across the inductor will reach its maximum a quarter cycle later.
3. Phase Relationship for Capacitor:
- For a capacitor, the voltage (V_C) lags the current (I) by a phase angle of π2 (or 90 degrees). This means that if the current is at its maximum, the voltage across the capacitor will reach its maximum a quarter cycle earlier.
4. Voltage Across L and C:
- Since the voltage across the inductor leads the current and the voltage across the capacitor lags the current, the voltages across L and C will be out of phase with each other. Specifically, the voltage across the inductor (V_L) and the voltage across the capacitor (V_C) will have a phase difference of 180 degrees (or π).
5. Conclusion for Voltage Statement:
- Therefore, the statement "the voltage across them is in phase" is False.
6. Current in Series Circuit:
- Since L and C are in series, the current flowing through both components is the same. Thus, the current in them is in phase.
7. Conclusion for Current Statement:
- Therefore, the statement "the current in them is in phase" is True.
Final Answers:
- Voltage across L and C is in phase: False
- Current in L and C is in phase: True
- In a series circuit, the same current flows through all components. Therefore, the current through the inductor (L) and the capacitor (C) is the same.
- For an inductor, the voltage (V_L) leads the current (I) by a phase angle of π2 (or 90 degrees). This means that if the current is at its maximum, the voltage across the inductor will reach its maximum a quarter cycle later.
- For a capacitor, the voltage (V_C) lags the current (I) by a phase angle of π2 (or 90 degrees). This means that if the current is at its maximum, the voltage across the capacitor will reach its maximum a quarter cycle earlier.
- Since the voltage across the inductor leads the current and the voltage across the capacitor lags the current, the voltages across L and C will be out of phase with each other. Specifically, the voltage across the inductor (V_L) and the voltage across the capacitor (V_C) will have a phase difference of 180 degrees (or π).
- Therefore, the statement "the voltage across them is in phase" is False.
- Since L and C are in series, the current flowing through both components is the same. Thus, the current in them is in phase.
- Therefore, the statement "the current in them is in phase" is True.
- Voltage across L and C is in phase: False
- Current in L and C is in phase: True
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Single Correct
63 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Solved Examples
6 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
find whether this is true (−21)×[(−4)+(−6)]=[(−21)×(−4)+[(−21)×(−6)]
View Solution_E01_735_Q01.png) True or False
True or False
View SolutionState True or false :
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
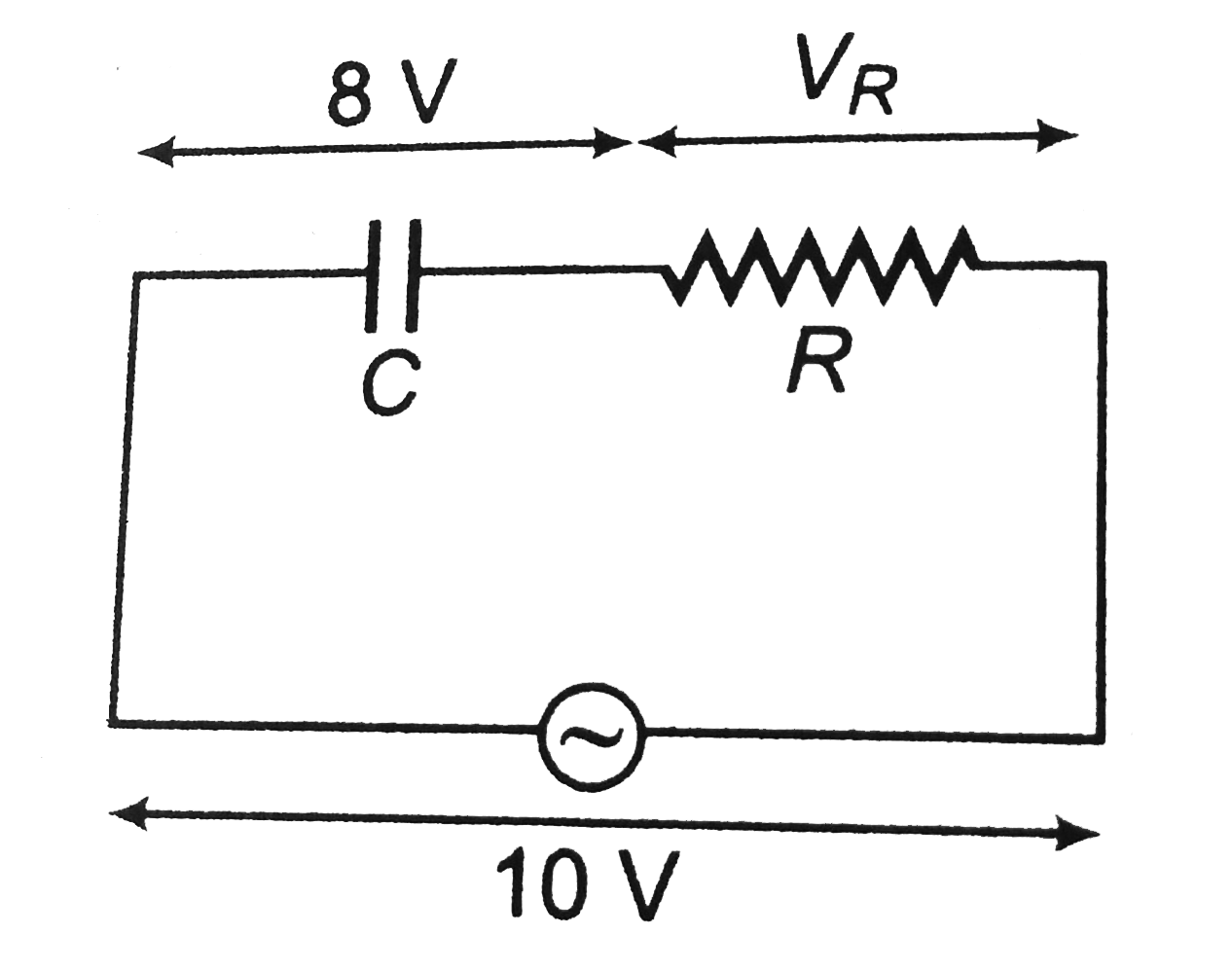 .
.
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
 .
.
View Solution(a) Draw graphs showing the variations of inductive reactnace and capacitive reactance with frequency of the applied ac source .
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c ) An alternating voltage of 220 V is applied across a device X , a current of 0.25 A flows , which lag behind the applied voltage in phase by π2 radian . If the same voltage is applied across another device Y , the same current flows but now it is in phase with the applied voltage .
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.

View SolutionAdsorption is exothermic. True/False
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View Solution
