When two bodies ofmasses m1 and m2 with specific heats s1 and s2 at absolute temperatures T10 and T20(T10>T20) are connected by a rod of length l and cross sectional area A with thermal conductivity k. Find the temperature difference of the bodies after time t. Neglect any heat loss due to radiation at any surface..

Let at time t after connecting the two bodies, they are at temperature, T1and T2 respectively(T1>T2). At this time, heat must be flowing from m1 tom2 asm1 is at higher temperature if dQ is the amount of heat flown through the rod from m1 to m2 and due to this if dT1 is fall in temperature of m1 and dT2 is rise in temperature of m2 then we have
dQ=−m1s1dT1 ..(4.17)
Also dQ=m2s2dT2 ....(4.18)
As this heat dQ is conducted through the rod , we have
dQdt=kA(T1)−T2l
or dQ=kAl(T1−T2)dt ...(4.19) As in this expression dQ is given as a function of(T1−T2). Thus from (4.17)and (4.18),we can get
dQ[1m1s1+1m2s2]=−d(T1−T2) ....(4.20)
Now from (4.19) and (4.20)
kA(T1−T2)l[1m1s1+1m2s2]dt=−d(T1−T2)
or d(T1−T2)T1−99T2=kAl[1m1s1+1m2s2]dt
Integrating the expression within proper limits, we get
∫T1−T2T10−T20d(T1−T2)(T1−T2)=−∫t0kAl(1m1s1+1m2s2)dt
In(T1−T2)(T10−T20)=−kAl(1m1s1+1m2s2)dt
or (T1−T2)=(T10−T20)e−kAl(1m1s2+1m2s2)t
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.10
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.11
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.8
1 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionFigure-4.13 shows a water tank at a constant temperature. T0 and a small bodyof mass m, and specific heat S at a temperature T1 . Given that T1<T0. A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.

View Solution
Knowledge Check
A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2A black body radiates heat at temperatures T1 and T2(T2>T1 the frequency corresponding to maxium energy is
Amore atT1Bmore at T2Cequal for T1 and T2Dindependent of T1 and T2If two bodies at different temperatures T1 and T2 are brought in thermal contact, the mean temperature T1+T22. When
Amass of two bodies are equalBpressure on two bodies are equalCtherma capacities of two bodies are equalDvolume of two bodies are equal
Two bodies each of mass m, having specific heats s, are connected by ametal rod of negligible heat capacity of length l, area of cross section A and thermal conductivity k. Initially both bodies are at different temperatures, find the time taken for the temperature difference between the two bodies to become half of the. initial value.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

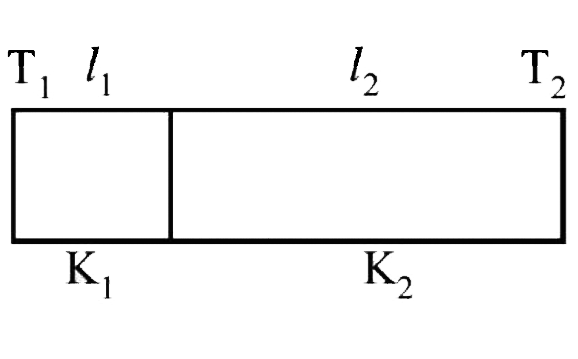
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionShown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
View SolutionTwo adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
View Solution
