When will the motion of a simple pendulum be simple harmonic?
Consider the diagram of a simple pendulum.
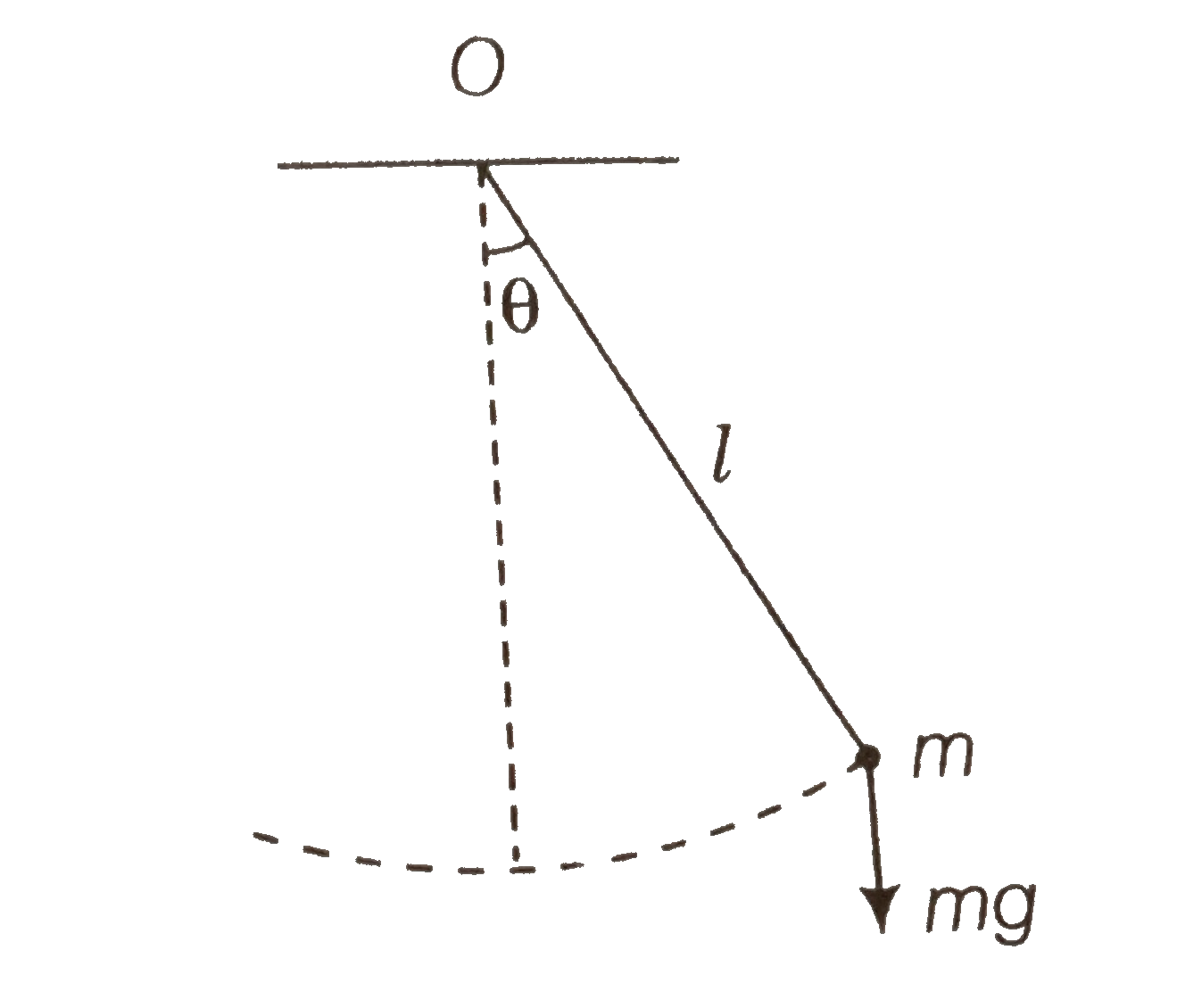
The bob is displaced through an angle 0 shown.
The restroing torque about the fixed point O is
τ=−mgsin0
If 0 is small angle in radians, then sin0≈0
⇒τ≈−mg0⇒τ∝(−0)
Hence, motion of a simple pendulum is SHM for small angle of oscillations.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The motion of a simple pendulum is
Aexactly simple harmonicBexactly rectilinearCapproximately simple harmonicDnone of theseAssertion: The motion of a simple pendulum is simple harmonic for all angular displacement.
Reason: Motion of simple pendulum is independent of the angular displacement.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.The length of a simple pendulum executing simple harmonic motion is increased by 21%. The percentage increase in the time period of the pendulum of increased length is
A0.11B0.21C0.42D10.5
Show that for small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression for its time period. Does it depend on the mass of the bob ?
View SolutionShow that the motion of simple pendulum is simple harmonic and hence derive an equation for its time period.What is Seconds pendulum?
View SolutionStatement-1 : The motion of a simple pendulum is not simple harmonic for large amplitudes.
Statement-2 : The restoring torque on a simple pendulum about the point of suspension is proportional to sinθ, where θ is the angular displacement of the pendulum.
View SolutionThe length of a simple pendulum executing simple harmonic motion is increased by 21%. The percentage increase in the time period of the pendulum of increased length is
View SolutionStatement-1 : The motion of simple pedulum is simple harmonic only for a <<l.
_E01_073_Q01.png)
Statement-2 : Motion of a simple pendulum is SHM for small angular displacement.
View Solution
