Which of the following particles will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field?
Electron
Proton
He+
Li++
The correct Answer is:Electron
To determine which particle will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field, we can use the formula for the radius of the circular path of a charged particle moving in a magnetic field:
r=mvqB
Where:
- r is the radius of the circular path,
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
1. Understand the Formula: The radius r is directly proportional to the mass m of the particle and the velocity v, and inversely proportional to the charge q and the magnetic field B. Since v, q, and B are constant for this problem, we can simplify our analysis to focus on the mass of the particles.
2. List the Particles and Their Masses:
- Electron: Mass me≈9.11×10−31 kg
- Proton: Mass mp≈1.67×10−27 kg
- Helium Positive Ion (He+): Mass mHe+≈4×mp≈6.68×10−27 kg
- Helium Two Positive Ion (He++): Mass mHe++≈4×mp≈6.68×10−27 kg
3. Compare the Masses: The electron has the smallest mass compared to the proton and the helium ions. The smaller the mass, the smaller the radius of the circular path, since r is directly proportional to m.
4. Conclusion: Since the electron has the smallest mass, it will describe the smallest circle when projected with the same velocity perpendicular to the magnetic field.
Final Answer:
The particle that will describe the smallest circle is the electron.
- r is the radius of the circular path,
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
- Electron: Mass me≈9.11×10−31 kg
- Proton: Mass mp≈1.67×10−27 kg
- Helium Positive Ion (He+): Mass mHe+≈4×mp≈6.68×10−27 kg
- Helium Two Positive Ion (He++): Mass mHe++≈4×mp≈6.68×10−27 kg
The particle that will describe the smallest circle is the electron.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - Exercises60videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - worked out Examples11videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
Which of the follwing particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
View SolutionWhich of the follwing particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
View SolutionWhich of the following particles will describe wll experience maximum magnetic force(magnitude) when projected with the same velocity perpendicular to a magnetic field?
View SolutionA proton and an alpha particle projected with same velocity in uniform transverse magnetic field then
View SolutionIf an electron and a proton having same momenta enter perpendicular to a magnetic field, then
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA proton moves at a speed v=2×106m/s in a region of constant magnetic field of magnitude B = 0.05 T. The direction of the proton when it enters this field is θ=30∘ to the field. When you look along the direction of the magnetic field, then the path is a circle projected on a plane perpendicular to the magnetic field. How far will the proton move along the direction of B when two projected circles have been completed?
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
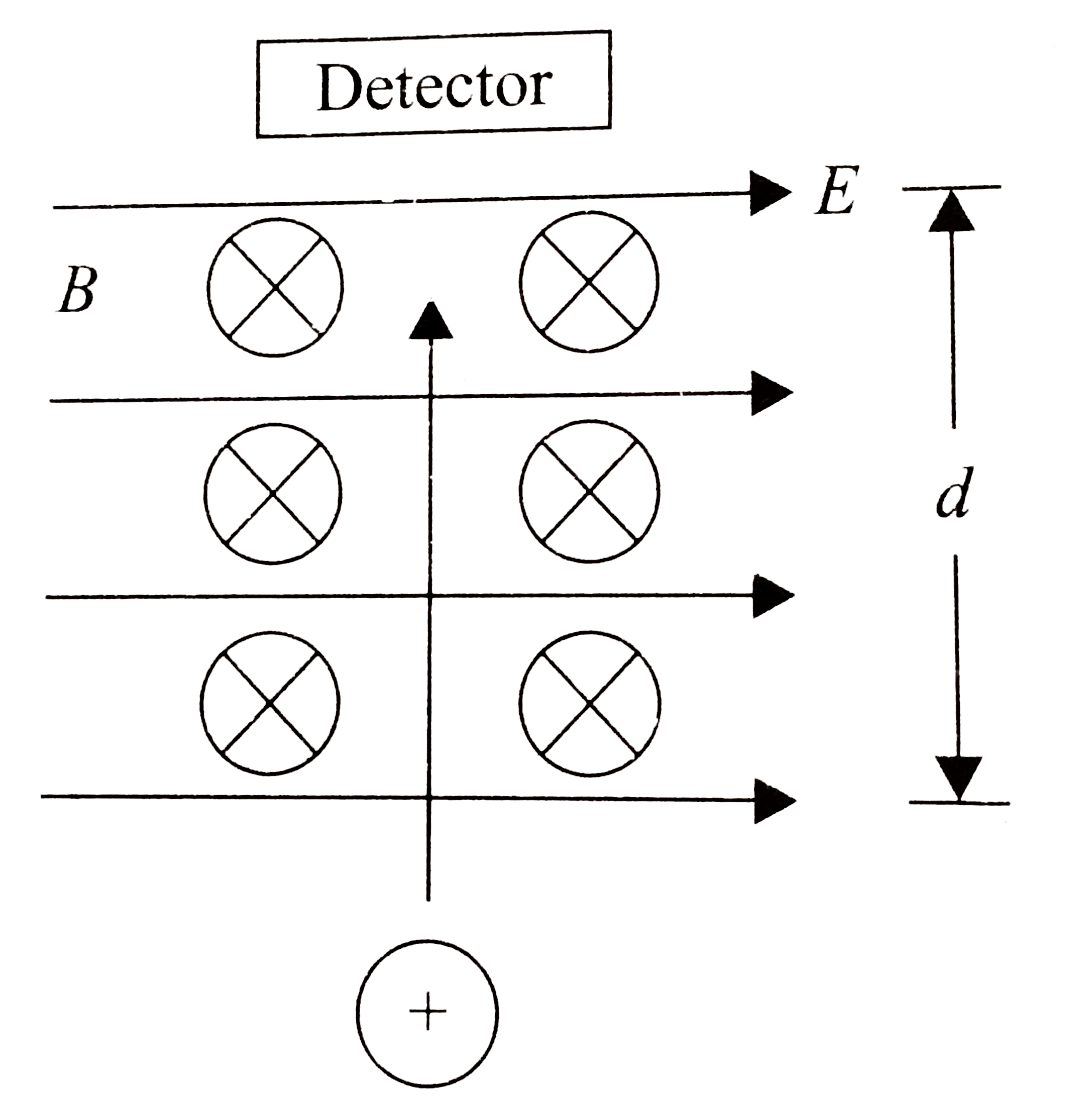
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?View SolutionStatement-1 A charged particle when projected perpendiculary to a uniform magnetic field, its velocity is constant through out its motion
Statement-2 A charged particle its acceleration is zero
Statement-3 A charged particle when projected perpendicular to a uniform magnetic field, a magnetic force acts on it but that does not change particle's speedView Solution

