Wind blows with a velocity in the direction shown in (Fig. 5.137). Two aeropalnes starts out from point and fly with a constant speed . The first flies from and the other . Both of them return back to . If , then which plane will return to point first, and what be the ratio of the times of flight of the two planes ?
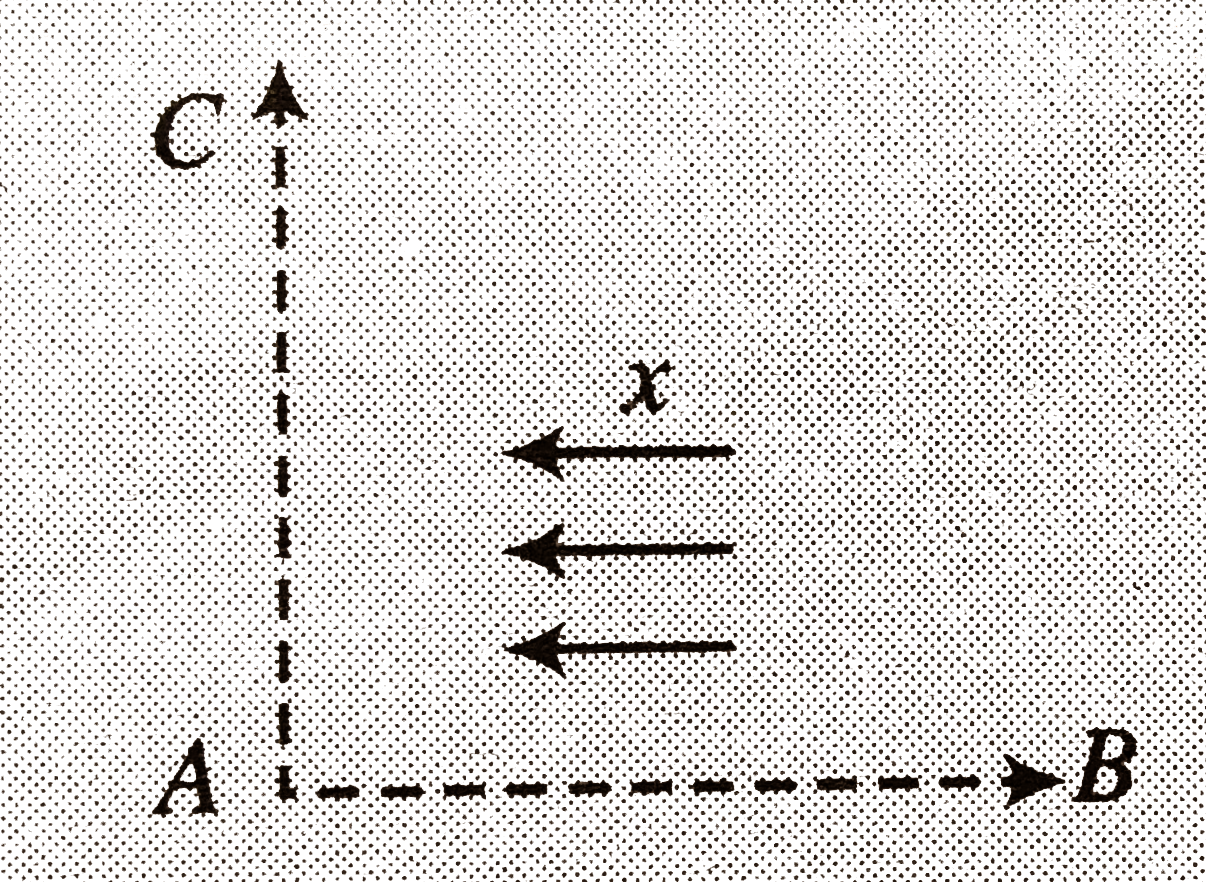 .
.
Time taken from to than to ,
Time taken from to than to ,
Ratio of times
Hence, the first plane takes more time.
 ,
,
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
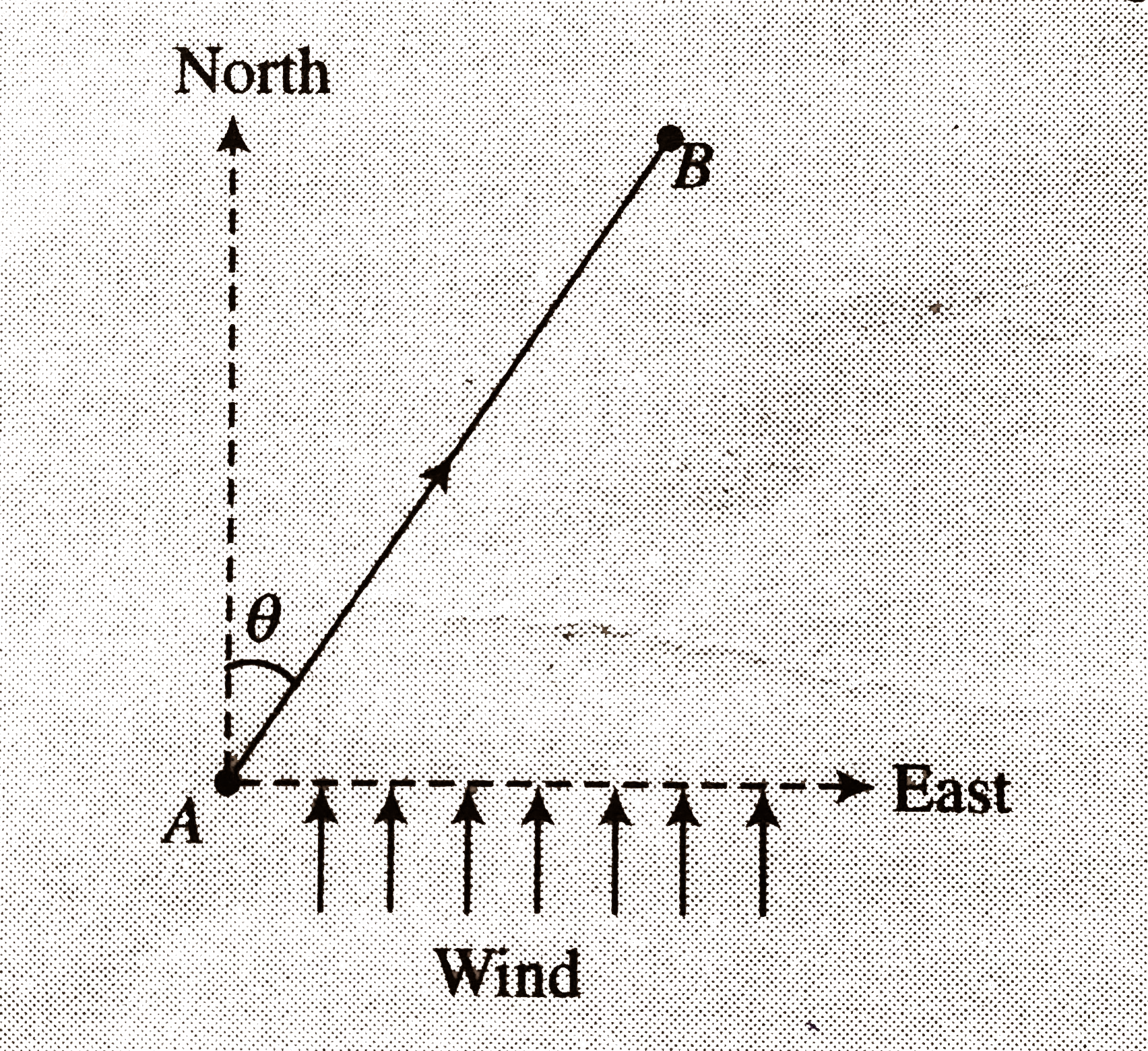
A helicopter files horizontally with constant velocity in a direction θ east of north between two points AandB, at distance d apart. Wind is blowing from south with constant speed u, the speed of helicopter relative to air is nu where n>1. find the speed of the helicopter along AB. The helicopter returns from B to A with same speed nu relative to air in same wind. Find the total time for the journeys.
 .
.
View SolutionTwo particles start moving simultaneously with constant velocities u1andu2 as shown in (Fig. 5.194). First particle starts from A along AO and second starts from O along OM. Find the shortest distance between them during their motion.
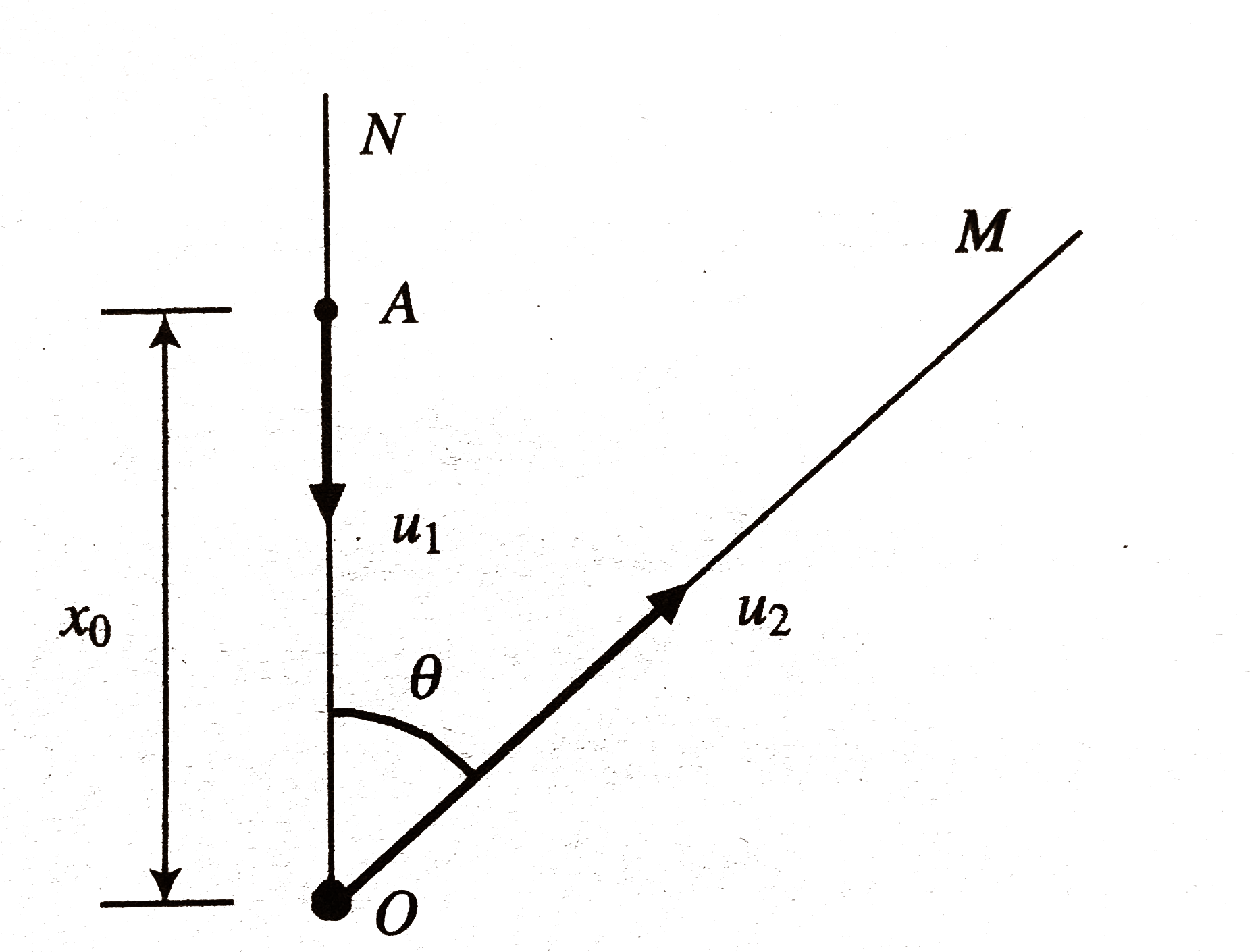 .
.
View Solution
Knowledge Check
Two bodies are projected from the same point with equal velocities in such a directions that they strike on the same point on a plane whose inclination is β. If α is the angle of projection of the first , the ration of there times of flight is
Asin(α−β):cosαBcosα:sin(α−β)Csinα+β:cosαDcosα:sin(α+β)In the Q. 122 what will be the velocity of the particle when it returns to the starting point?
A→r0B−→r0C2→r0D−2→r0Two trains A and B travel from points X to Y and the ratio of the speeds of A to that of B is 2 : 7. Find the ratio of time taken by A and B to reach from X to Y.
A2:5B3:5C3:8D7:2
Wind is blowing at constant velocity →v towards west. A man initially at rest starts moving with constant acceleration →a towards north. The moment of time at which direction of wind appears south west to him is:
View SolutionThree persons start walking from A to B .The ratio of their speed is 4:3:5 .Find the ratio of their time to rach at the point B ?
View SolutionThe distance between two points (A and B is 110 km. X starts running from point A at a speed of 60 km/hr and Y starts running from point B at a speed of 50 km/hr at the same time. They meet at a point C, somewhere on the line AB. What is the ratio of AC to BC?
View SolutionTwo planes start from a city and fly in opposite directions, one averaging a speed of 40 km/h greater than the others. If they are 3400 km apart after 5 h. Their average speeds are
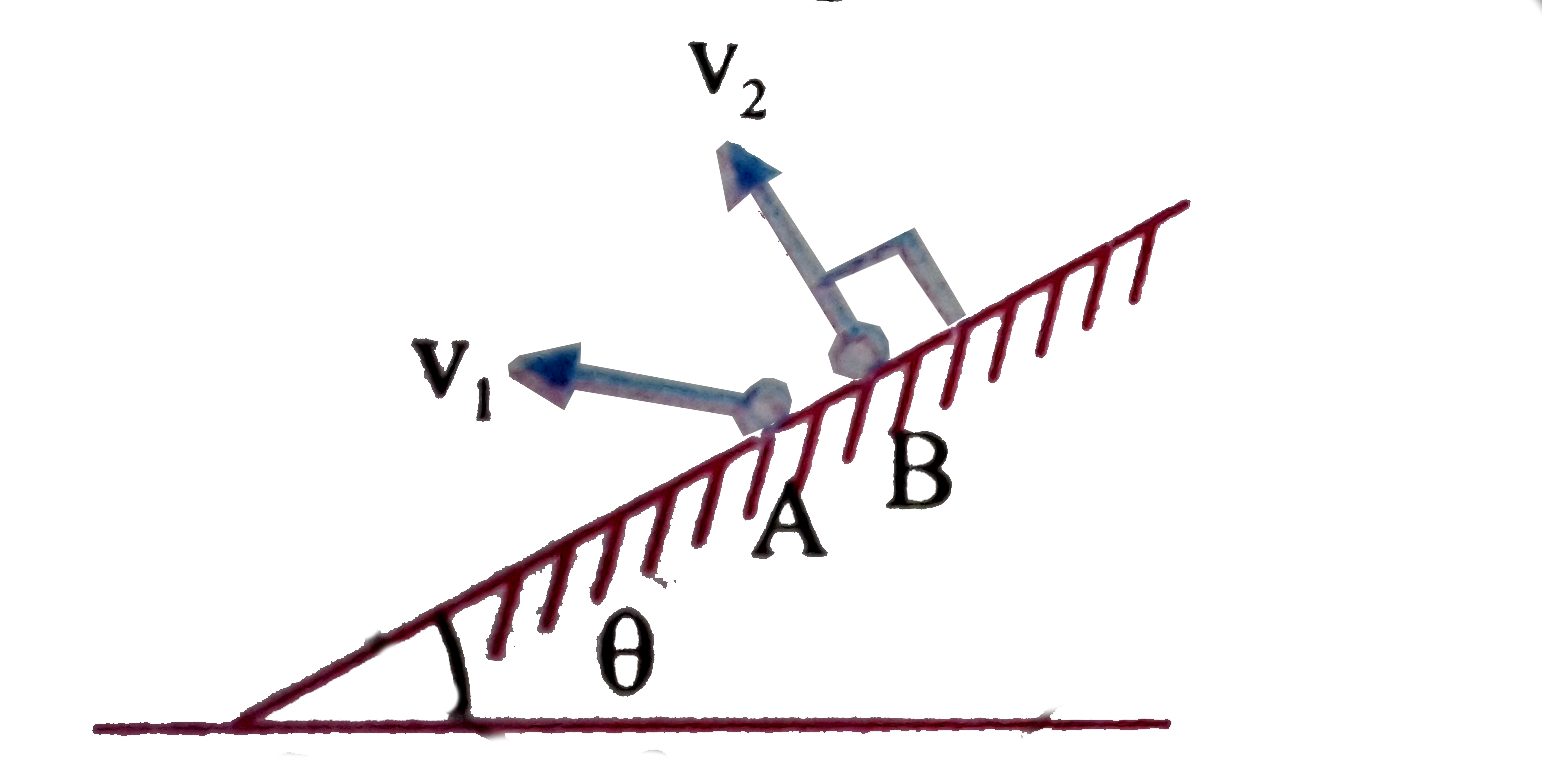
View SolutionTwo bodies AandB are projected from the same place in same vertical plane with velocities v1andv2.Form a long inclined plane as shown Find the ratio of their times of flight.
View Solution
