With what minimum speed v must a small ball should be pushed inside a smooth vertical tube from a height h so that it may reach the top of the tube? Radius of the tube is R .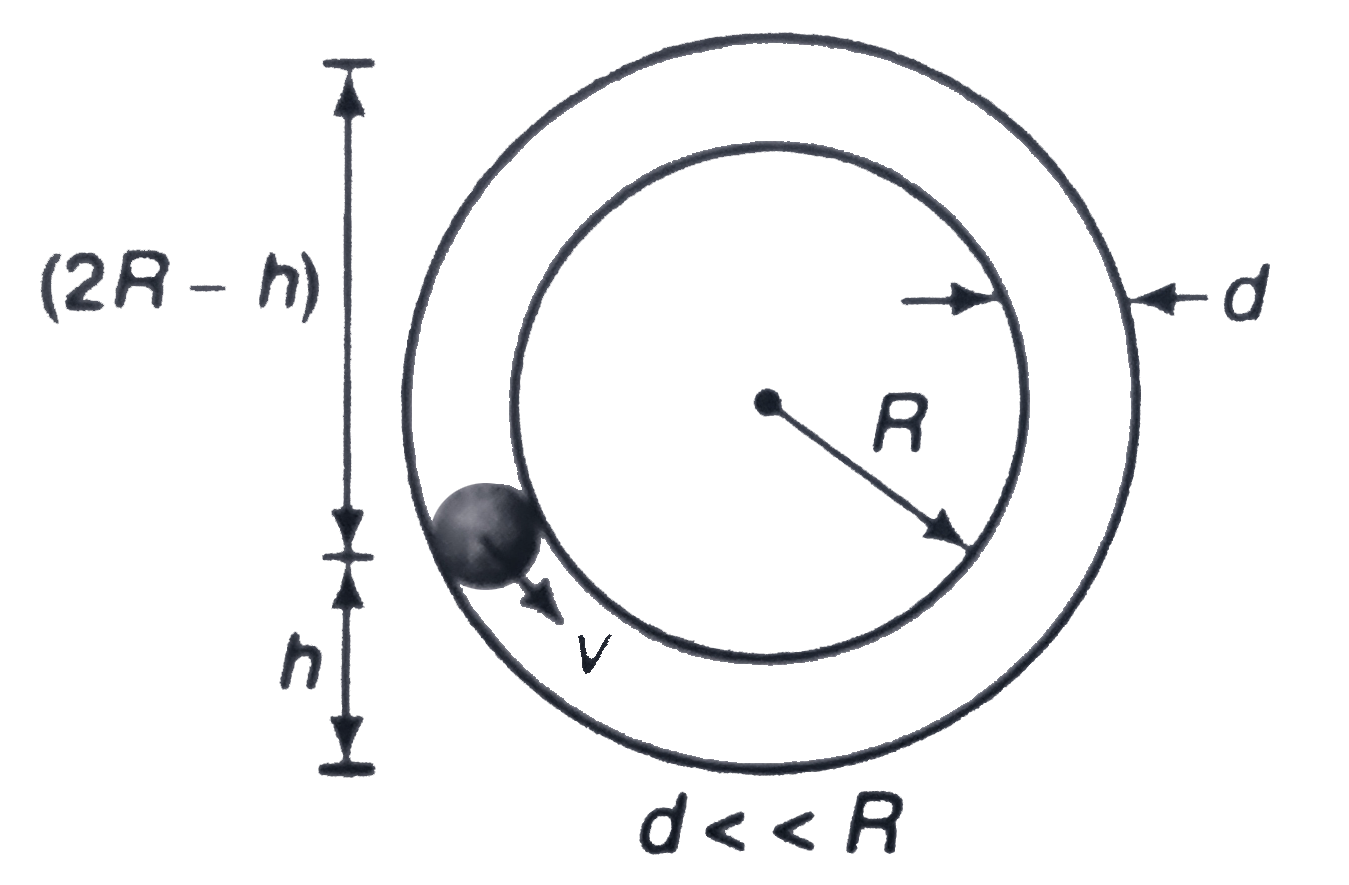 
√2g(h+2R)
52R
√g(5R−2h)
√2g(2R−h)
The correct Answer is:D
Velocity of ball to just reach the top of the tube should be given by:
0=v2−2gh0
Here h0=(R−h)
and in critical case velocity will be zero at topmost point.
Thus v=√2g(2R−h)
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision31videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts32videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power25videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
With what minimum speed v must a small ball should be pushed inside a smooth vertical tube from a heoght h so that it may reach the top of the tube? Radius of the tube is R .
View SolutionA ball is released from top of the smooth vertical, when i just leaves the contract form inner surface of the tube
_PHY_223_Q01.png)
View Solution
Knowledge Check
- Question 1 - Select One
A capillary tube is dipped in water and the water rises in it to a height h . If r be the radius of the bore of the tube , then
Ah∝rBh∝1/rCh∝r2Dh∝1/r2 - Question 2 - Select One
A small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
A√2ghB√2g(R+h)C√2g(R−h)DNone of these - Question 3 - Select One
In a vertical smooth hollow thin tube, a block of same mass as that of tube is released as shown. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, the displacement of the tube will be (where ‘R’ is the mean radius of tube, assume that the tube remains in vertical plane).
A2RπB4RπCR2DR
A smooth circular tube is held in a vertical position. A small ball which is free to slide inside the tube is held stationary at the highest position in the tube. If the ball is slightly displaced from its position of rest, show that the force exerted by the ball on the wall of the tube is given as mg(3cosθ−2) , where m is the mass of the ball and θ is the angular displacement from highest position. Upto what value of θ , this result will remain valid.
View SolutionA ball is thrown upwards with speed ‘v’ from the top of a tower and it reaches the ground with a speed 3v, then the height of the tower is
View SolutionA large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View SolutionA capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
View SolutionA capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
View Solution