Work done in time t on a body of mass m which is accelerated from rest to a speed v in time t1 as a function of time t is given by
12mv2t21t2
12(mvt1)2t2
mvt1t2
12mvtt2
The correct Answer is:A
To solve the problem of finding the work done on a body of mass m that is accelerated from rest to a speed v in time t1, we can follow these steps:
1. Identify Initial Conditions:
- The body has a mass m.
- It starts from rest, so the initial velocity u=0.
- It reaches a final speed v in time t1.
2. Calculate Acceleration:
- Using the equation of motion:
v=u+at
Since u=0, we have:
v=at1
- Rearranging gives us the acceleration a:
a=vt1
3. Calculate Displacement:
- The displacement s during the time t1 can be calculated using the formula:
s=ut+12at2
Again, since u=0:
s=12at21
- Substituting the value of a:
s=12(vt1)t21=12vt1
4. Calculate Work Done:
- The work done W on the body is given by:
W=Force×Displacement
- The force F can be calculated using Newton's second law:
F=ma=m(vt1)
- Therefore, substituting for force and displacement:
W=F⋅s=(mvt1)⋅(12vt1)
- Simplifying this gives:
W=12mv⋅v=12mv2
5. Final Expression:
- The work done in time t on the body is:
W=12mv2
- The body has a mass m.
- It starts from rest, so the initial velocity u=0.
- It reaches a final speed v in time t1.
- Using the equation of motion:
v=u+at
Since u=0, we have:
v=at1
- Rearranging gives us the acceleration a:
a=vt1
- The displacement s during the time t1 can be calculated using the formula:
s=ut+12at2
Again, since u=0:
s=12at21
- Substituting the value of a:
s=12(vt1)t21=12vt1
- The work done W on the body is given by:
W=Force×Displacement
- The force F can be calculated using Newton's second law:
F=ma=m(vt1)
- Therefore, substituting for force and displacement:
W=F⋅s=(mvt1)⋅(12vt1)
- Simplifying this gives:
W=12mv⋅v=12mv2
- The work done in time t on the body is:
W=12mv2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
An automobile of mass m accelerates from rest. If the engine supplies a constant power P, the velocity at time t is given by -
View SolutionA body of mass m is acceleratad uniformaly from rest to a speed v in a time T . The instanseous power delivered to the body as a function of time is given by
View Solution
Knowledge Check
A body of mass m accelerates uniformly from rest to v1 in time t1. As a function of time t, the instantaneous power delivered to the body is
Amv1tt1Bmv21tt1Cmv1t2t1Dmv21tt21
Under the action of a force a 2 kg body moves such that its position x in meters as a function of time t is given by x=t44+3. Then work done by the force in first two seconds is
View SolutionA body of mass m, accelerates uniformly from rest to V1 in time t1. The instantaneous power delivered to the body as a function of time t is.
View SolutionThe displacement x of a body of mass 1 kg on a horizontal smooth surface as a function of time t is given by x=t44. The work done in the first second is
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA car of mass m is initially at rest on the boat of mass M tied to the wall of dock through a massless, inextensible string. The car accelerates from rest to velocity v0 in times to. At t=t0 the car applies brake and comes to rest relative to the boat in negligible time. Neglect friction between the boat and water: the time 't' at which boat will strike the wall is
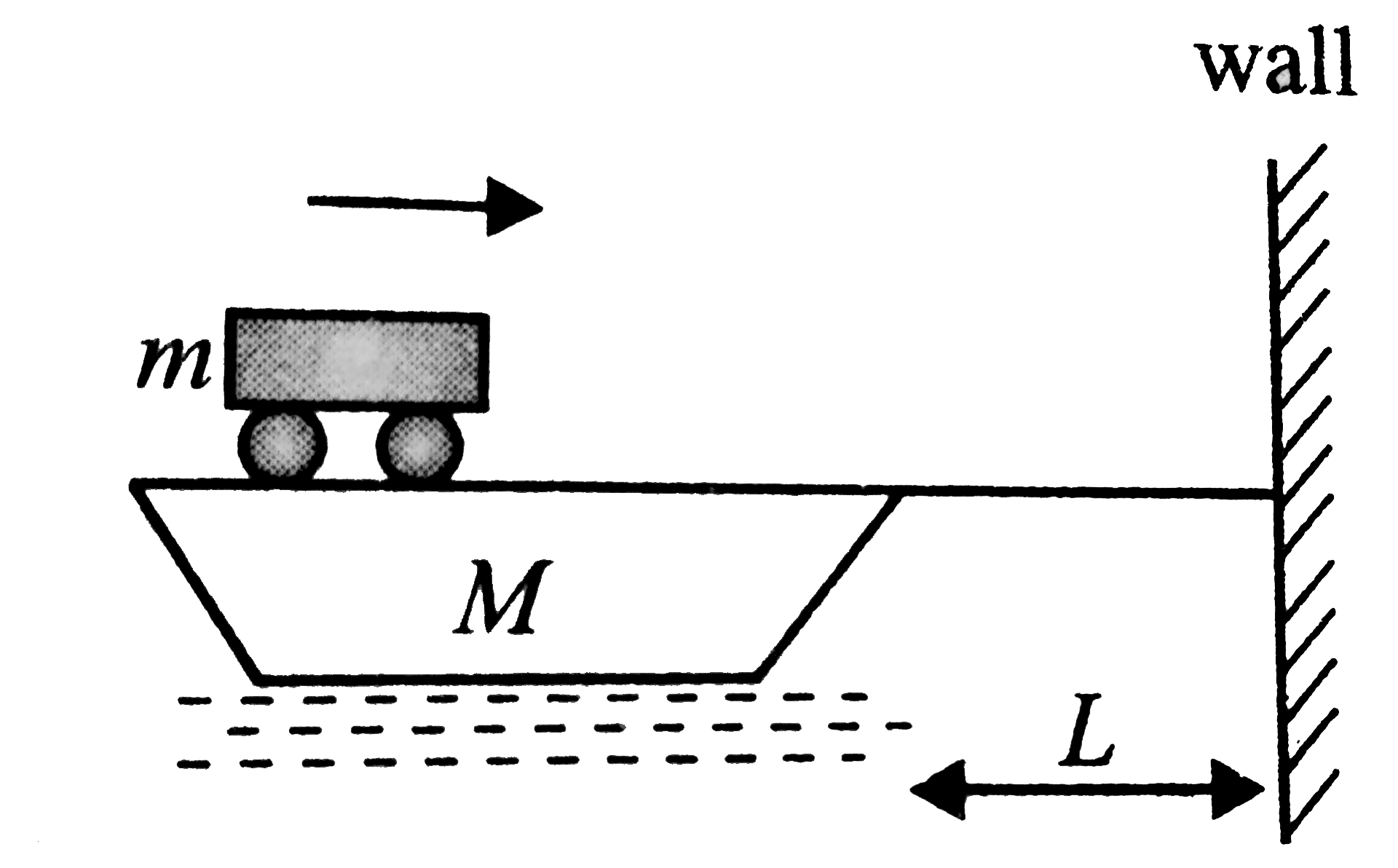
View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
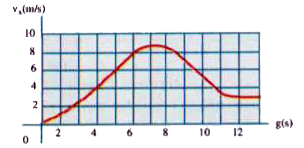
View SolutionGraph of velocity (v) versus time 't' for motion of a motorbike which starts from rest and moves along a stright road is given .
(a)Find the average acceleration for the time interval t0=0 to t1=6.0 s
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration is zero ?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
View Solution
