A body of mass m=3.90 kg slides on a horizontal frictionless table with a speed of v=120 ms−1. It is brought to rest in compressing a spring in its path. How much does spring is compressed, if its force constant k is 135 Nm−1?
0.204 m
0.408 m
0.804 m
4.04 m
The correct Answer is:A
To solve the problem, we need to find out how much the spring is compressed when a body of mass m=3.90kg sliding with a speed v=1.20m/s comes to rest after compressing the spring with a spring constant k=135N/m.
1. Identify the Energy Types:
- The body has kinetic energy (KE) when it is moving.
- When the body compresses the spring, the kinetic energy is converted into potential energy (PE) stored in the spring.
2. Write the Kinetic Energy Formula:
KE=12mv2
where:
- m=3.90kg
- v=1.20m/s
3. Calculate the Kinetic Energy:
KE=12×3.90×(1.20)2
KE=12×3.90×1.44
KE=2.7952J
4. Write the Potential Energy Formula for the Spring:
PE=12kx2
where x is the compression of the spring.
5. Set the Kinetic Energy Equal to the Potential Energy:
Since all the kinetic energy is converted into potential energy:
12mv2=12kx2
6. Cancel Out the 12:
mv2=kx2
7. Rearrange to Solve for x2:
x2=mv2k
8. Substitute the Known Values:
x2=3.90×(1.20)2135
x2=3.90×1.44135
x2=5.616135
x2≈0.0417
9. Take the Square Root to Find x:
x=√0.0417≈0.204m
Final Answer:
The spring is compressed by approximately x≈0.204m.
- The body has kinetic energy (KE) when it is moving.
- When the body compresses the spring, the kinetic energy is converted into potential energy (PE) stored in the spring.
KE=12mv2
where:
- m=3.90kg
- v=1.20m/s
KE=12×3.90×(1.20)2
KE=12×3.90×1.44
KE=2.7952J
PE=12kx2
where x is the compression of the spring.
Since all the kinetic energy is converted into potential energy:
12mv2=12kx2
mv2=kx2
x2=mv2k
x2=3.90×(1.20)2135
x2=3.90×1.44135
x2=5.616135
x2≈0.0417
x=√0.0417≈0.204m
The spring is compressed by approximately x≈0.204m.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA 2 kg block slides on a horizontal floor with a speed of 4 m/s. It strikes an uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is 15 N and spring constant is 10000 N/m. The spring is compressed by (in cm):
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
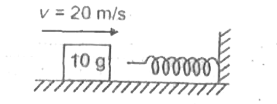
View SolutionA solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be
(Force constant of the spring = 36 N/m)
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View Solution
