Write an expression for the centre of mass of& two partide system
To derive the expression for the center of mass of a two-particle system, we can follow these steps:
Step 1: Define the particles and their positions
Let’s denote two particles with masses m1 and m2. The position of the first particle is given by →r1 and the position of the second particle is given by →r2.
Step 2: Understand the concept of center of mass
The center of mass (COM) of a system is the point where the total mass of the system can be considered to be concentrated. For a two-particle system, the center of mass can be calculated using the weighted average of their positions.
Step 3: Write the formula for the center of mass
The formula for the center of mass →R of a two-particle system is given by:
→R=m1→r1+m2→r2m1+m2
Step 4: Explanation of the formula
- The numerator m1→r1+m2→r2 represents the total momentum of the system, where each position vector is weighted by its corresponding mass.
- The denominator m1+m2 is the total mass of the system.
Step 5: Conclusion
Thus, the center of mass of a two-particle system is the point that balances the masses of the two particles in relation to their positions.
---
Let’s denote two particles with masses m1 and m2. The position of the first particle is given by →r1 and the position of the second particle is given by →r2.
The center of mass (COM) of a system is the point where the total mass of the system can be considered to be concentrated. For a two-particle system, the center of mass can be calculated using the weighted average of their positions.
The formula for the center of mass →R of a two-particle system is given by:
- The numerator m1→r1+m2→r2 represents the total momentum of the system, where each position vector is weighted by its corresponding mass.
- The denominator m1+m2 is the total mass of the system.
Thus, the center of mass of a two-particle system is the point that balances the masses of the two particles in relation to their positions.
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesFind the distance between centre of gravity and centre of mass of a two particle system attached to the ends of a light rod. Each particle has same mass. Length of the rod is R, where R is the radius of earth.
_E01_014_Q01.png) ARBR/2CzeroDR/4
ARBR/2CzeroDR/4
Find out the position of centre of mass of two particle system.
View SolutionCalculate centre of mass of the system
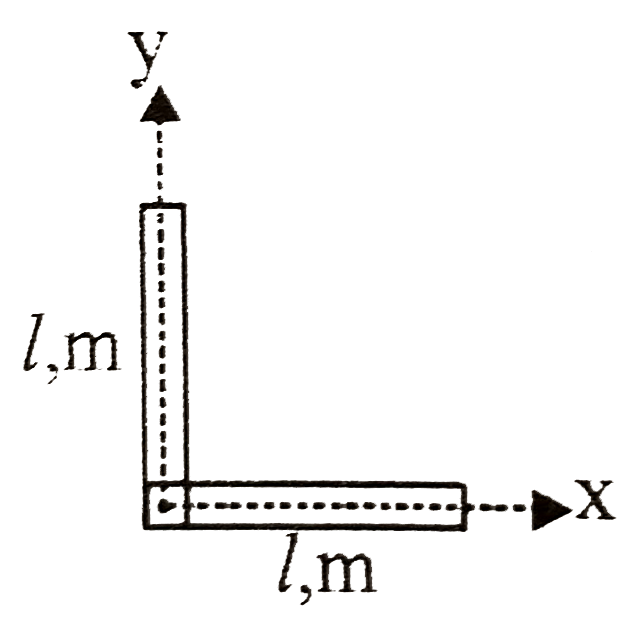
View SolutionWrite an expression for the position vector of the centre of mass of n-particle system. Also write the equations of motion which govern the motion of the centre of mass
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionWhere does the centre of mass of a two particle system lie, if one particle ismore massive than the other ?
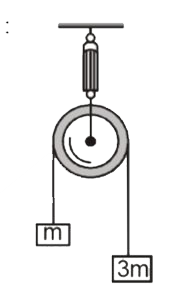
View SolutionIf the system is released, then the acceleration of the centre of mass of the system :
View Solution
