Write expression for the magnetic flux density at a point due to a current carrying wire of:
an infinite length?Solution in Punjabi
Consider a long straight wire LM.
Let I = Current flowing through the wire from L to M.
Let P be the observation point, where we want to calculate the magnetic field.
OP = a = Perpendicular distance of P from the current carrying wire
Consider the small element CD of length dl of the wire and I is distance of mid-point of elementary portion CD from O.
r = OʻP = Distance of mid-point of small elementary portion CD from P.
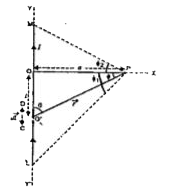
0 = Angle between the current carrying wire and the line joining the mid-point of CD to P, i.e., between →dl and →r .
According to Biot-Savart.s law, magnetic induction −→dB at the point P due to small current element CD is given by
−→dB=μ04πI→dl׈rr2
In magnitude dB=μ04πIdlsinθr2 ...(1)
and sinθ=dr=cosθ .....(2)
or r=acosϕ=asecϕ ....(3)
Also , tanϕ=l/aorl=atanϕ ....(4)
dl=asec2ϕdϕ
Substituting the values from eqns. (2), (3) and (4) in eqn. (1), we get
dB=μ04πI(asec2ϕdϕ)cosϕa2sec2ϕ
dB=μ0I4πacosϕdϕ ....(5)
Join PM and PL. Let ∠OPM.=ϕ2 and ∠OPL=−ϕ1
Then, magnetic field due to the whole length of conductor LM can be calculated by integrating eqn. (5) within the limits −ϕ1 to −ϕ2. Thus,
B=∫ϕ2−ϕ1dB=μ0I4πa∫ϕ2−ϕ1cosϕdϕ
=μ0I4πa[sinϕ]−θ2−θ1=μ0I4πa[sinϕ2−sin(ϕ1)]
=μ0I4πa[sinϕ2+sinϕ1] ....(6)
The above expression gives the magnitude of the magnetic field due to current carrying straight conductor of finite length.
If the conductor is infinitely long and the point P lies near the centre of the conductor, then
ϕ1=ϕ2=π2
So, B=μ0I4πa[sinπ2+sinπ2]
B=μ02I4πa
It is the expression for magnetic field due to an infinitely long current carrying straight conductor.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - NUMERICALS PROBLEMS3videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - SHORT ANSWER TYPE QUESTIONS4videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC DIPOLES AND EARTH'S MAGNETISMEXERCISE - Most Expected Questions8videos
MAGNETIC DIPOLES AND EARTH'S MAGNETISM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - NUCLEAR REACTIONSEXERCISE - Numerical Problems9videos
NUCLEAR REACTIONS
Similar Questions
A current of 15A flows through a coil Magnetic field at centre of semi-circular loop of 5.0 cm radius as shown in fig. Find out the direction and magnitude of magnetic field at the centre of the arc.
 00:57View Solution
00:57View SolutionExplain Biot-Savart law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
02:22View SolutionWhat do you mean by Neutral Point in a magnetic field?
03:58View SolutionIt is given that each fission of a chain reaction produces 200 MeV energy. What is the number of fissions taking place per second it the reactor produces 1012W Power ?
02:05View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
02:47View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
06:36View SolutionWrite the expression for magnetic flux at one end of a long solenoid carrying current.
03:43View SolutionGive the expression for magnetic flux density at a point due to an infinitely long conductor perpendicular to it.
13:44View SolutionGive the expression for magnetic flux density, at a point on the axis, due to a current carrying circular conductor.
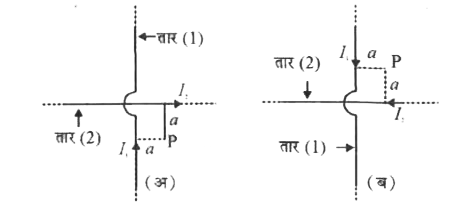
View Solutionचित्र में प्रदर्शित दो अनन्त लम्बाई के धारावाही चालक तारों के कारण बिंदु P पर परिणामी चुम्बकीय क्षेत्र ज्ञात कीजिए।
 03:03View Solution
03:03View SolutionUsing Ampere.s circuital law derive an expression for magnetic field due to infinitely long current carrying wire at a point at distance Yfrom it.
06:19View SolutionDerive an expression for the magnetic field due to an infinitely long straight wire carrying current I.
05:05View SolutionWrite the expression for the magnetic field produced by an infinitely straight wire carrying a current I at a short perpendicular distance a from itself.
02:22View SolutionA famous law in physics is expressed as ointbarB.bar(dl)=mu_0I Using the above get an expression for the intensity of magnetic field at a point due to an infinite current carrying wire.
04:39View Solutionएम्पियर का परिपथीय नियम लिखिये । इसे गणितीय रूप में व्यक्त कीजिये, इसके उपयोग से, अनन्त लम्बाई के, किसी धारा वाही चालक के कारण, चुम्बकीय क्षेत्र के मान के लिये एक व्यंजक प्राप्त कीजिये ।
05:57View SolutionWrite expression for the magnetic flux density at a point due to a current carrying wire of: a finite length?
02:03View Solution

