Write the vector form of force acting between two charges q1andq2 having →r1and→r2 as their position vectors respectively.
To find the vector form of the force acting between two charges q1 and q2 with position vectors →r1 and →r2 respectively, we can follow these steps:
1. Identify the Charges and Position Vectors:
Let q1 and q2 be two point charges located at position vectors →r1 and →r2.
2. Determine the Vector Distance:
The vector distance →r between the two charges can be expressed as:
→r=→r2−→r1
3. Calculate the Magnitude of the Distance:
The magnitude of the vector distance r is given by:
r=|→r|=|→r2−→r1|
4. Apply Coulomb's Law:
According to Coulomb's Law, the force →F12 acting on charge q1 due to charge q2 is given by:
→F12=kq1q2r2^r
where k is Coulomb's constant and ^r is the unit vector in the direction of →r.
5. Express the Unit Vector:
The unit vector ^r in the direction of →r is given by:
^r=→r|→r|=→r2−→r1|→r2−→r1|
6. Substitute the Unit Vector into the Force Equation:
Now substituting ^r into the force equation:
→F12=kq1q2|→r2−→r1|2⋅→r2−→r1|→r2−→r1|
7. Final Vector Form of the Force:
Thus, the final vector form of the force acting on charge q1 due to charge q2 is:
→F12=kq1q2|→r2−→r1|3(→r2−→r1)
Let q1 and q2 be two point charges located at position vectors →r1 and →r2.
The vector distance →r between the two charges can be expressed as:
→r=→r2−→r1
The magnitude of the vector distance r is given by:
r=|→r|=|→r2−→r1|
According to Coulomb's Law, the force →F12 acting on charge q1 due to charge q2 is given by:
→F12=kq1q2r2^r
where k is Coulomb's constant and ^r is the unit vector in the direction of →r.
The unit vector ^r in the direction of →r is given by:
^r=→r|→r|=→r2−→r1|→r2−→r1|
Now substituting ^r into the force equation:
→F12=kq1q2|→r2−→r1|2⋅→r2−→r1|→r2−→r1|
Thus, the final vector form of the force acting on charge q1 due to charge q2 is:
→F12=kq1q2|→r2−→r1|3(→r2−→r1)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- ELECTROSTATICSBOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - LONG ANSWER TYPE QUESTIONS
14 Videos
- Electromagnetic WavesBOOK - MBD -HARYANA BOARDCHAPTER - Electromagnetic WavesEXERCISE - Example
7 Videos
- MAGNETISMBOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - OBJECTIVE TYPE QUESTIONS
17 Videos
Similar Questions
Find the expression for the potential energy of a system of two point charges q1,andq2 glocated at →r1and→r2 respectively in an external electric field →E.
(b) Draw equipotential surfaces due to an isolated point charge (-q) and depict the electric field lines.
(c) Three point charges +1μC,−1μCand+2μC are initially infinite distance apart. Calculate the work done in assembling these charges at the vertices of an equilateral triangle of side 10 cm.
View SolutionDeduce the expression for the electric filed →E due to a system of two charges q1andq2 with position vectors →r1and→r2 at a point P having position vector →®.
View Solution
Knowledge Check
The positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
A→r1√q1+→r2√q2√q1+√q2B→r1√q2+→r2√q1√q1+√q2C→r1√q2+→r2√q1√q1+q2D→r1√q1+→r2√q2√q1+q2Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1The electrostatic force between two point charges q1 and q2 at separation r is given by F=k.q1q2r2. The constant k
ADepends upon system of units onlyBDepends upon medium between the chargesCDepends on both 1 and 2DIs independent of both 1 and 2
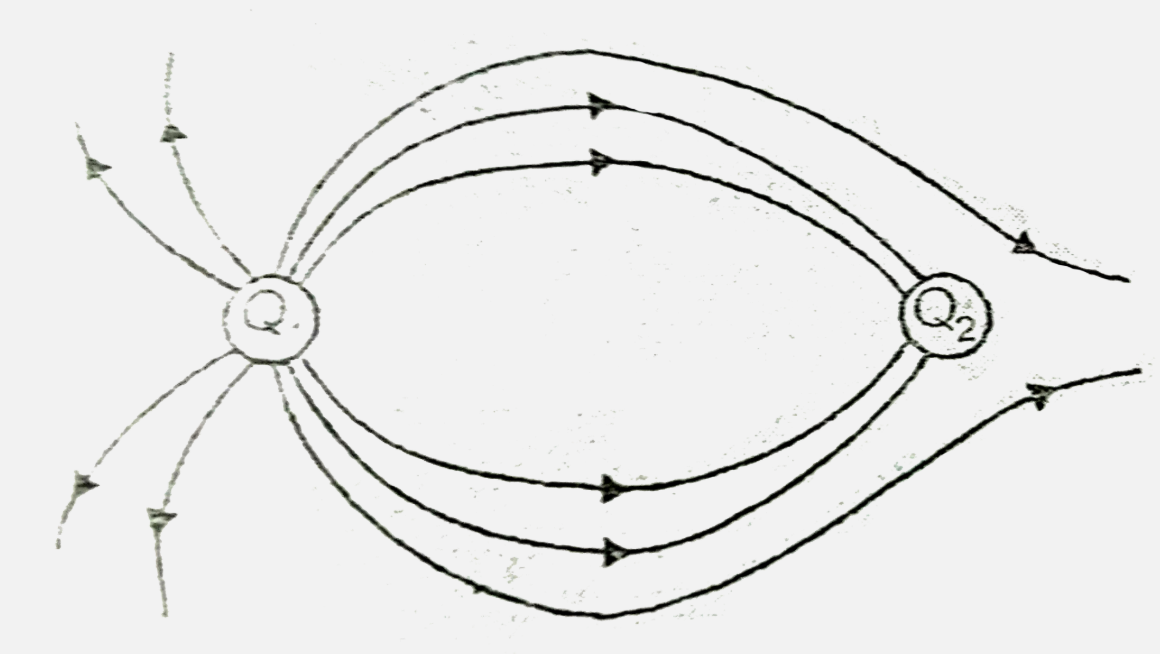
Looking at the various electric lines of forces between charges Q1 and Q2, find the value of Q1Q2.
View SolutionCalculate the electrostatic potential energy of a system of three point charges q1,q2 and q3 located respectively at →r1,→r2 and →r3 with respect to a common origin O.
View SolutionFind force acting between two shells of radius R1 and R2 which have uniformly distributed charges Q1 and Q2 respectively and distance between their centres is r.

View SolutionThe force of interaction between two charges q1=6μC and q2=2μCis 12N .If charge q=−2μC is added to each of the charges,then the new force of interaction is
View SolutionIs the force acting between two point charges q1andq2 kept at some distance in air, attractive or repulsive when:
(i)q1q2>0
(ii)q1q2<0
View Solution
