Find the expression for the potential energy of a system of two point charges $q_{1}, and q_{2}$ glocated at ${\to r}_{1} and {\to r}_{2}$ respectively in an external electric field $\to E .$
(b) Draw equipotential surfaces due to an isolated point charge (-q) and depict the electric field lines.
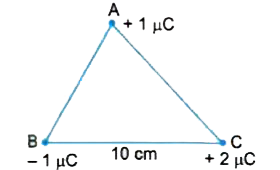
(c) Three point charges $+ 1 μ C, - 1 μ C and + 2 μ C$ are initially infinite distance apart. Calculate the work done in assembling these charges at the vertices of an equilateral triangle of side 10 cm.

Text Solution

Verified by Experts

(a) To find the potential energy of a system of two point charges ${\to r}_{1} and {\to r}_{2}$ situated at points and respectively in an external electric field $\to E$ , first we calculate the work done in bringing the charge $q_{1}$ . from infinity to ${\to r}_{1}$ . Work done in this step is
$W_{1} = q_{1} V ({\to r}_{1}), where V ({\to r}_{1})$ is the electrostatic potential at ${\to r}_{1}$ .
Now we consider the work done in bringing $q_{2} to {\to r}_{2}$ . In this step work W, is done against the electric field and work $W_{2}$ is done against the field due to charge $q_{1} .$ Obviously
$W_{2} = q_{2} V ({\to r}_{2}), where V ({\to r}_{2})$ is the electrostatic potential at ${\to r}_{2}$
and $W_{12} = \frac{q_{1} q_{2}}{4 π ε_{0} . r_{12}} where r_{12} = | {\to r}_{1} - {\to r}_{2} |$ = distance between $q_{1} and q_{2}$
Total work done in bringing $q_{2} to {\to r}_{2} = W_{2} + W_{12} = q_{2} V ({\to r}_{2}) + \frac{q_{1} q_{2}}{4 π \in_{0} . r_{12}}$
Potential energy of the system U.
= The total work done in assembling the configuration
$U = W_{1} + W_{2} + W_{12} = q_{1} V (r_{1}) + q_{2} V (r_{2}) + \frac{q_{1} q_{2}}{4 π ε_{0} . r_{12}}$
(b) Equipotential surfaces due to an isolated point charge-q are drawn here and electric field lines have been depicted.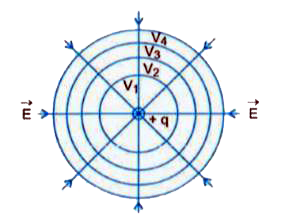
(c) Hence $q_{1} = + 1 μ C = + 1 \times 10^{- 6} C, q_{2} = - 1 μ C = - 1 \times 10^{- 6} C, q_{3} = + 2 μ C = + 2 \times 10^{- 6} C and r_{12} = r_{13} = r_{23} = 10 c m = 0.1 m$
Work done is assembling the charges =Potential energy of charge alignment
$W = U = \frac{1}{4 π ε_{0}} [\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}}]$

$= 9 \times 10^{9} [(1 \times 10^{- 6}) \times \frac{- 1 \times 10^{- 6}}{0.1} + (1 \times 10^{- 6}) \times \frac{2 \times 10^{- 6}}{0.1} + (- 1 \times 10^{- 6}) \times \frac{2 \times 10^{- 6}}{0.1}]$
=0.09J

Updated on:21/07/2023

The positions of two point charges $q_{1}$ and $q_{2}$ are ${\to r}_{1}$ and ${\to r}_{2}$ , respectively. Find the position of the point where the net field is zero due to thses charges.
A $\frac{{\to r}_{1} \sqrt{q_{1}} + {\to r}_{2} {\sqrt{q}}_{2}}{{\sqrt{q}}_{1} + {\sqrt{q}}_{2}}$
B $\frac{{\to r}_{1} \sqrt{q_{2}} + {\to r}_{2} {\sqrt{q}}_{1}}{{\sqrt{q}}_{1} + {\sqrt{q}}_{2}}$
C $\frac{{\to r}_{1} \sqrt{q_{2}} + {\to r}_{2} {\sqrt{q}}_{1}}{\sqrt{q_{1} + q_{2}}}$
D $\frac{{\to r}_{1} \sqrt{q_{1}} + {\to r}_{2} {\sqrt{q}}_{2}}{\sqrt{q_{1} + q_{2}}}$
The two point charges $4 μ C$ and $1 μ C$ are separated by a distance of 2 m in air. Find the point on the line joining the charges at which net electric field of the system is zero.
A $\frac{4}{3} m$ from $1 μ C$
B $\frac{2}{3} m$ from $1 μ C$
C $\frac{4}{3} m$ from $4 μ C$
D $\frac{2}{3} m$ from $4 μ C$