x-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
To find the unit vector along the refracted ray when a ray of light passes from one medium to another, we can follow these steps:
Step 1: Define the Incident Ray Vector
The incident ray is given as a vector:
→I=^i+^j−^k
Step 2: Calculate the Unit Vector of the Incident Ray
To find the unit vector ^e1 along the incident ray, we need to divide the incident ray vector by its magnitude. The magnitude of →I is calculated as follows:
|→I|=√12+12+(−1)2=√1+1+1=√3
Thus, the unit vector ^e1 is:
^e1=→I|→I|=^i+^j−^k√3=1√3(^i+^j−^k)
Step 3: Identify the Refractive Indices
The refractive index of the first medium (z>0) is given as μ1=1 and for the second medium (z<0), it is μ2=2.
Step 4: Define the Normal Vector
The normal vector ^n is directed along the z-axis:
^n=^k
Step 5: Apply Snell's Law in Vector Form
Snell's law in vector form is given by:
μ1^e1×^n=μ2^e2×^n
Substituting the known values:
1⋅(1√3(^i+^j−^k))×^k=2^e2×^k
Step 6: Calculate the Cross Product
Calculating the left-hand side:
^e1×^n=(1√3(^i+^j−^k))×^k=1√3(^i×^k+^j×^k−^k×^k)
Using the right-hand rule:
^i×^k=−^j,^j×^k=^i,^k×^k=0
Thus,
^e1×^n=1√3(−^j+^i)=1√3(^i−^j)
Step 7: Set Up the Equation for ^e2
Now we have:
1√3(^i−^j)=2^e2×^k
Assuming ^e2=x^i+y^j+z^k, we find:
^e2×^k=x^i×^k+y^j×^k+z^k×^k=−y^i+x^j
Thus, we have:
1√3(^i−^j)=2(−y^i+x^j)
Step 8: Equate the Coefficients
Equating coefficients gives us:
1√3=−2yand−1√3=2x
From these, we can solve for x and y:
y=−12√3,x=−14√3
Step 9: Find the z-component
Using the unit vector condition:
x2+y2+z2=1
Substituting x and y:
(−14√3)2+(−12√3)2+z2=1
Calculating:
148+112+z2=1⟹z2=1−(148+448)=1−548=4348
Thus, z=−√4348 (since the ray is refracted downwards).
Step 10: Write the Final Unit Vector
The unit vector along the refracted ray ^e2 is:
^e2=−14√3^i−12√3^j−√4348^k
Final Answer
The unit vector along the refracted ray is:
^e2=−14√3^i−12√3^j−√4348^k
The incident ray is given as a vector:
→I=^i+^j−^k
To find the unit vector ^e1 along the incident ray, we need to divide the incident ray vector by its magnitude. The magnitude of →I is calculated as follows:
|→I|=√12+12+(−1)2=√1+1+1=√3
Thus, the unit vector ^e1 is:
^e1=→I|→I|=^i+^j−^k√3=1√3(^i+^j−^k)
The refractive index of the first medium (z>0) is given as μ1=1 and for the second medium (z<0), it is μ2=2.
The normal vector ^n is directed along the z-axis:
^n=^k
Snell's law in vector form is given by:
μ1^e1×^n=μ2^e2×^n
Substituting the known values:
1⋅(1√3(^i+^j−^k))×^k=2^e2×^k
Calculating the left-hand side:
^e1×^n=(1√3(^i+^j−^k))×^k=1√3(^i×^k+^j×^k−^k×^k)
Using the right-hand rule:
^i×^k=−^j,^j×^k=^i,^k×^k=0
Thus,
^e1×^n=1√3(−^j+^i)=1√3(^i−^j)
Now we have:
1√3(^i−^j)=2^e2×^k
Assuming ^e2=x^i+y^j+z^k, we find:
^e2×^k=x^i×^k+y^j×^k+z^k×^k=−y^i+x^j
Thus, we have:
1√3(^i−^j)=2(−y^i+x^j)
Equating coefficients gives us:
1√3=−2yand−1√3=2x
From these, we can solve for x and y:
y=−12√3,x=−14√3
Using the unit vector condition:
x2+y2+z2=1
Substituting x and y:
(−14√3)2+(−12√3)2+z2=1
Calculating:
148+112+z2=1⟹z2=1−(148+448)=1−548=4348
Thus, z=−√4348 (since the ray is refracted downwards).
The unit vector along the refracted ray ^e2 is:
^e2=−14√3^i−12√3^j−√4348^k
The unit vector along the refracted ray is:
^e2=−14√3^i−12√3^j−√4348^k
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.412videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.522videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.220videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A ray of light in incident along a vector ˆi+ˆj−ˆk on a plane mirror lying in y-z plane. The unit vector along the reflected ray can be
View SolutionThe x−y plane is the boundary between two transparent media. Medium-1 with z≤0 has a refractive index √2 and medium -2 with z≤0 has a refractive index √2. A ray of light in medium -1 given by vector A=√3ˆi−ˆk is incident on the plane of separation. The unit vector in the direction of the refracted ray in medium-2 is
View SolutionA ray of light is incident on a plane mirror along a vector ˆi+ˆj−ˆk.
The normal on incidence point is along ˆi+ˆj.Find a unit vector along the
reflected ray.View SolutionA ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….View SolutionLet the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
View SolutionA beam of monochromatic light is refracted from vacuum into a medium of refractive index 1.5 The wavelength of refracted light will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA thin lens made of a material of refractive indexμ2 has a medium of refractive index μ1 on one side and a medium of refractive index on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium p, and (b) from the medium μ3?
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
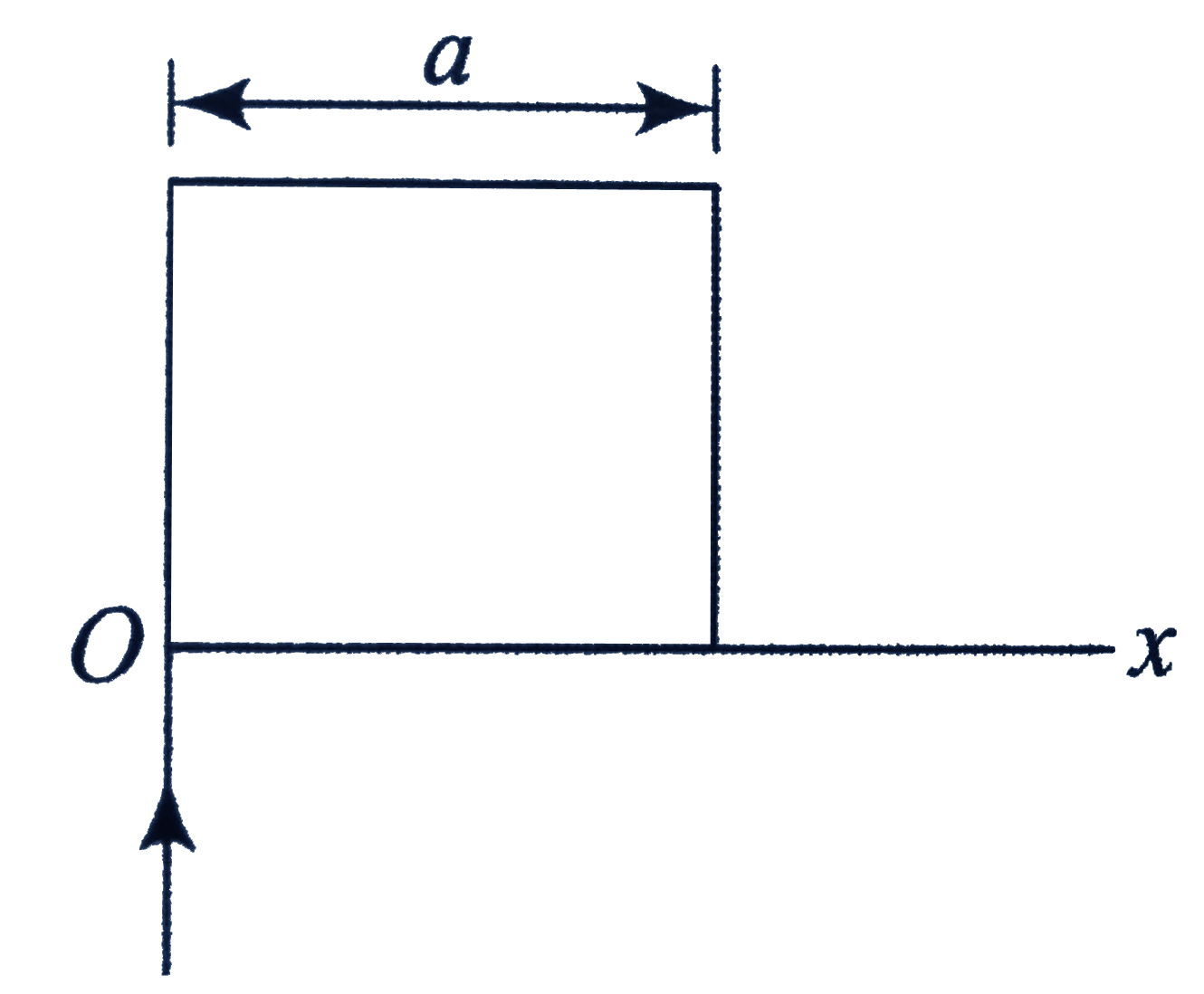 View Solution
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
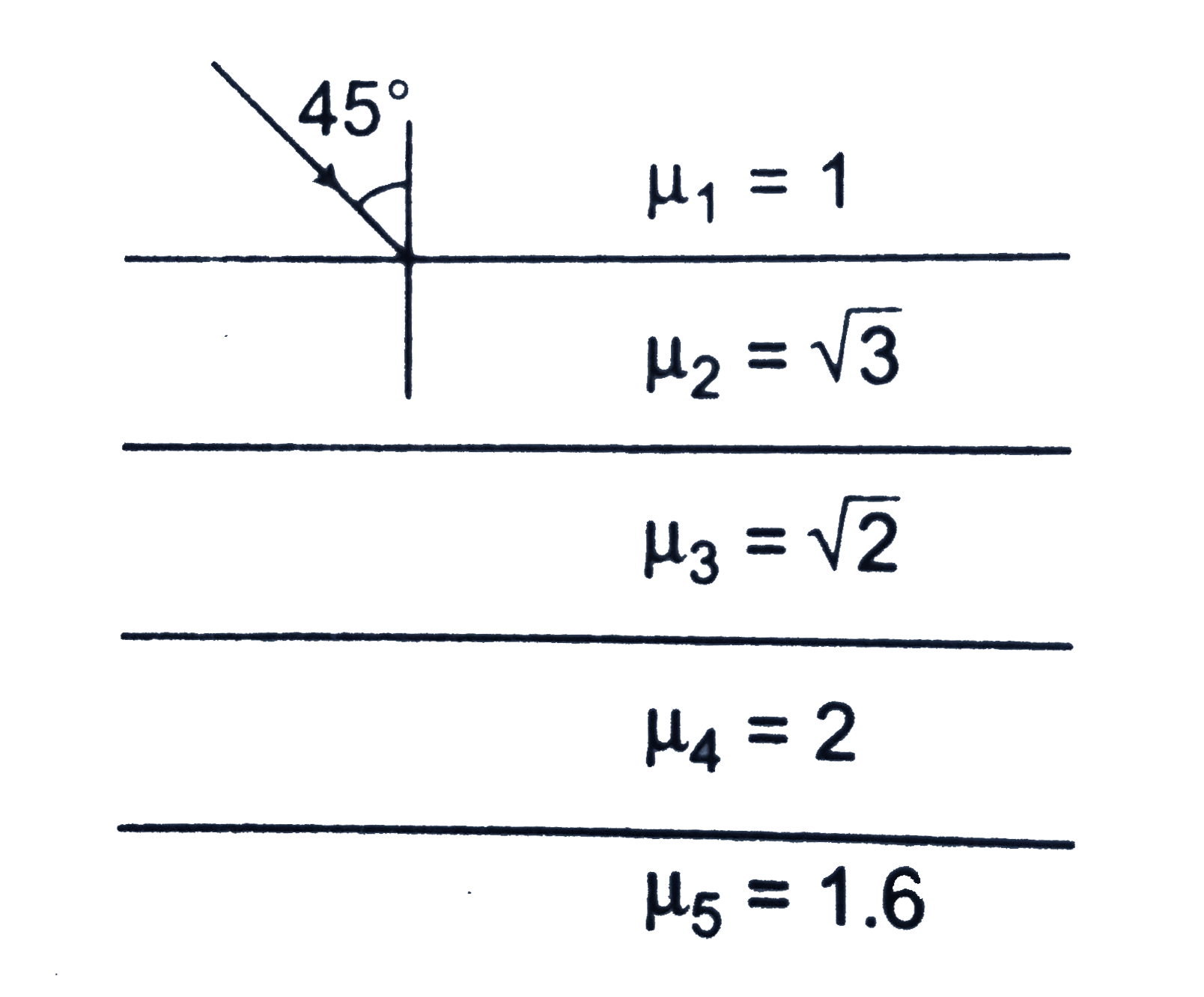 View Solution
View Solution

