The plane is the boundary between two transparent media. Medium-1 with has a refractive index and medium -2 with has a refractive index . A ray of light in medium -1 given by vector is incident on the plane of separation. The unit vector in the direction of the refracted ray in medium-2 is
The correct Answer is:C
To solve the problem, we need to find the unit vector in the direction of the refracted ray in medium-2 when a ray of light is incident from medium-1.
1. Identify the Given Information:
- Refractive index of medium-1, n1=√2
- Refractive index of medium-2, n2=√2
- Incident ray vector in medium-1, A=√3^i−^k
2. Determine the Angle of Incidence:
- The direction of the incident ray can be expressed as a vector. The incident ray vector is given by A=√3^i−^k.
- The components of the incident ray are:
- Ax=√3
- Ay=0
- Az=−1
- The angle of incidence i can be found using the tangent function:
tan(i)=AzAx=−1√3
- Therefore, i=tan−1(−1√3), which corresponds to −45∘ or 135∘.
3. Apply Snell's Law:
- According to Snell's law:
n1sin(i)=n2sin(r)
- Since n1=n2, we have:
sin(i)=sin(r)
- This implies that r=i. Therefore, the angle of refraction r is also −45∘ or 135∘.
4. Determine the Direction of the Refracted Ray:
- Let the unit vector of the refracted ray be B=x^i+y^j+z^k.
- Since the angle of refraction r=−45∘, we have:
tan(r)=yx=−1⟹y=−x
- The z-component of the refracted ray will be determined by the symmetry of the media. Since the media are symmetrical, we can assume z remains the same as the incident ray, which is −1.
5. Normalize the Refracted Ray Vector:
- The refracted ray vector can be expressed as:
B=x^i−x^j−^k
- To find the magnitude:
|B|=√x2+(−x)2+12=√2x2+1
- To find the unit vector, we need to normalize B:
Unit vector=B|B|
6. Choose a Value for x:
- Let x=1√2 (to simplify calculations):
B=1√2^i−1√2^j−^k
- The magnitude becomes:
|B|=
⎷2(1√2)2+12=√1+1=√2
- Therefore, the unit vector in the direction of the refracted ray is:
Bunit=1√2^i−1√2^j−1√2^k
Final Answer:
The unit vector in the direction of the refracted ray in medium-2 is:
Bunit=1√2^i−1√2^j−^k
- Refractive index of medium-1, n1=√2
- Refractive index of medium-2, n2=√2
- Incident ray vector in medium-1, A=√3^i−^k
- The direction of the incident ray can be expressed as a vector. The incident ray vector is given by A=√3^i−^k.
- The components of the incident ray are:
- Ax=√3
- Ay=0
- Az=−1
- The angle of incidence i can be found using the tangent function:
tan(i)=AzAx=−1√3
- Therefore, i=tan−1(−1√3), which corresponds to −45∘ or 135∘.
- According to Snell's law:
n1sin(i)=n2sin(r)
- Since n1=n2, we have:
sin(i)=sin(r)
- This implies that r=i. Therefore, the angle of refraction r is also −45∘ or 135∘.
- Let the unit vector of the refracted ray be B=x^i+y^j+z^k.
- Since the angle of refraction r=−45∘, we have:
tan(r)=yx=−1⟹y=−x
- The z-component of the refracted ray will be determined by the symmetry of the media. Since the media are symmetrical, we can assume z remains the same as the incident ray, which is −1.
- The refracted ray vector can be expressed as:
B=x^i−x^j−^k
- To find the magnitude:
|B|=√x2+(−x)2+12=√2x2+1
- To find the unit vector, we need to normalize B:
Unit vector=B|B|
- Let x=1√2 (to simplify calculations):
B=1√2^i−1√2^j−^k
- The magnitude becomes:
|B|=
⎷2(1√2)2+12=√1+1=√2
- Therefore, the unit vector in the direction of the refracted ray is:
Bunit=1√2^i−1√2^j−1√2^k
The unit vector in the direction of the refracted ray in medium-2 is:
Bunit=1√2^i−1√2^j−^k
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
Let the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View Solution
Knowledge Check
The refractive index of a medium is √3. What is the angle of refraction, if unpolarizing light is incident on the polarising angle of the medium ?
A60∘B45∘C30∘D0∘
A ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….
View SolutionThe speed of light in a transparent medium is 0.6 times that of its speed in vacuum. What is the refractive index of the medium?
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
View SolutionA ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
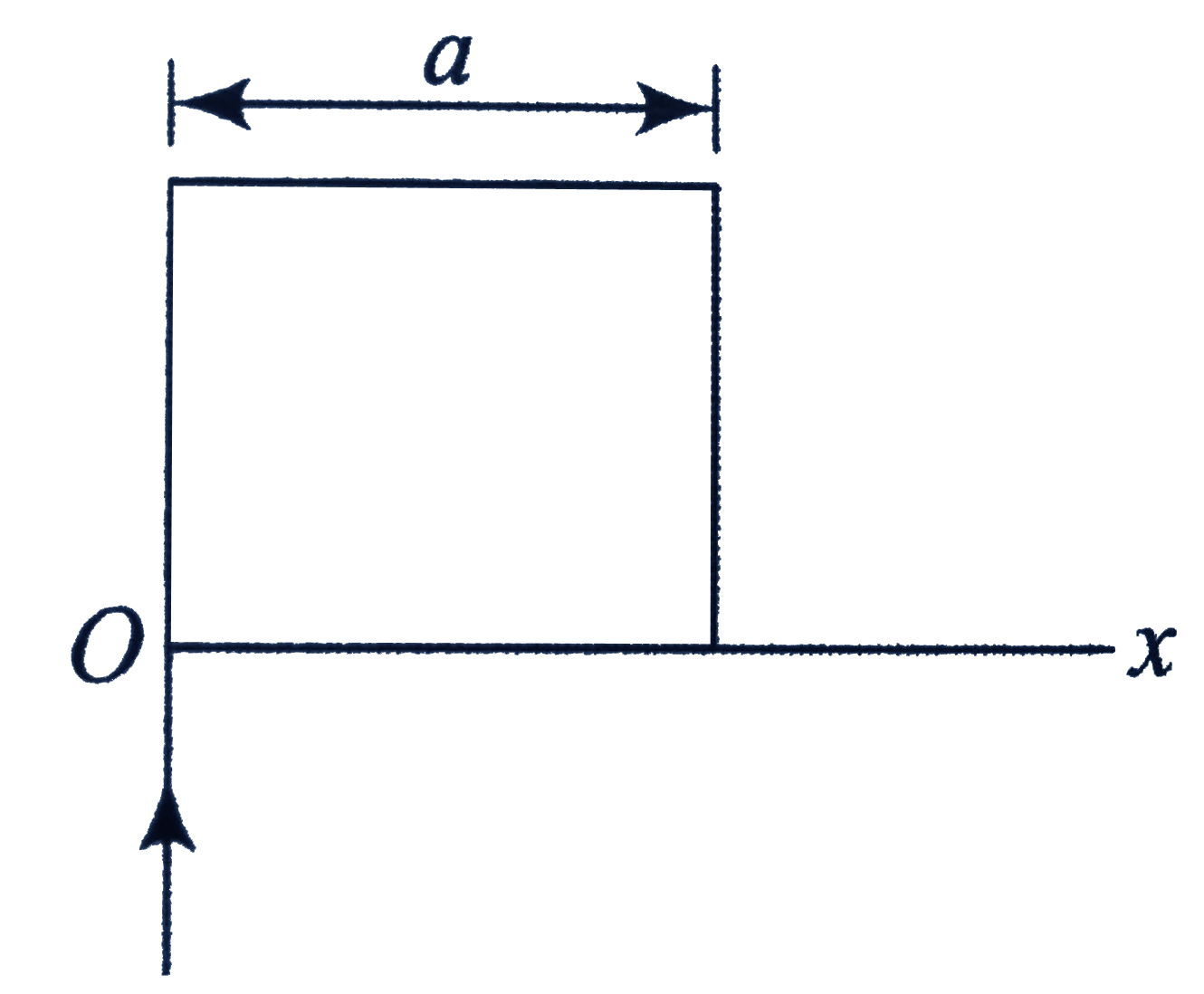
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
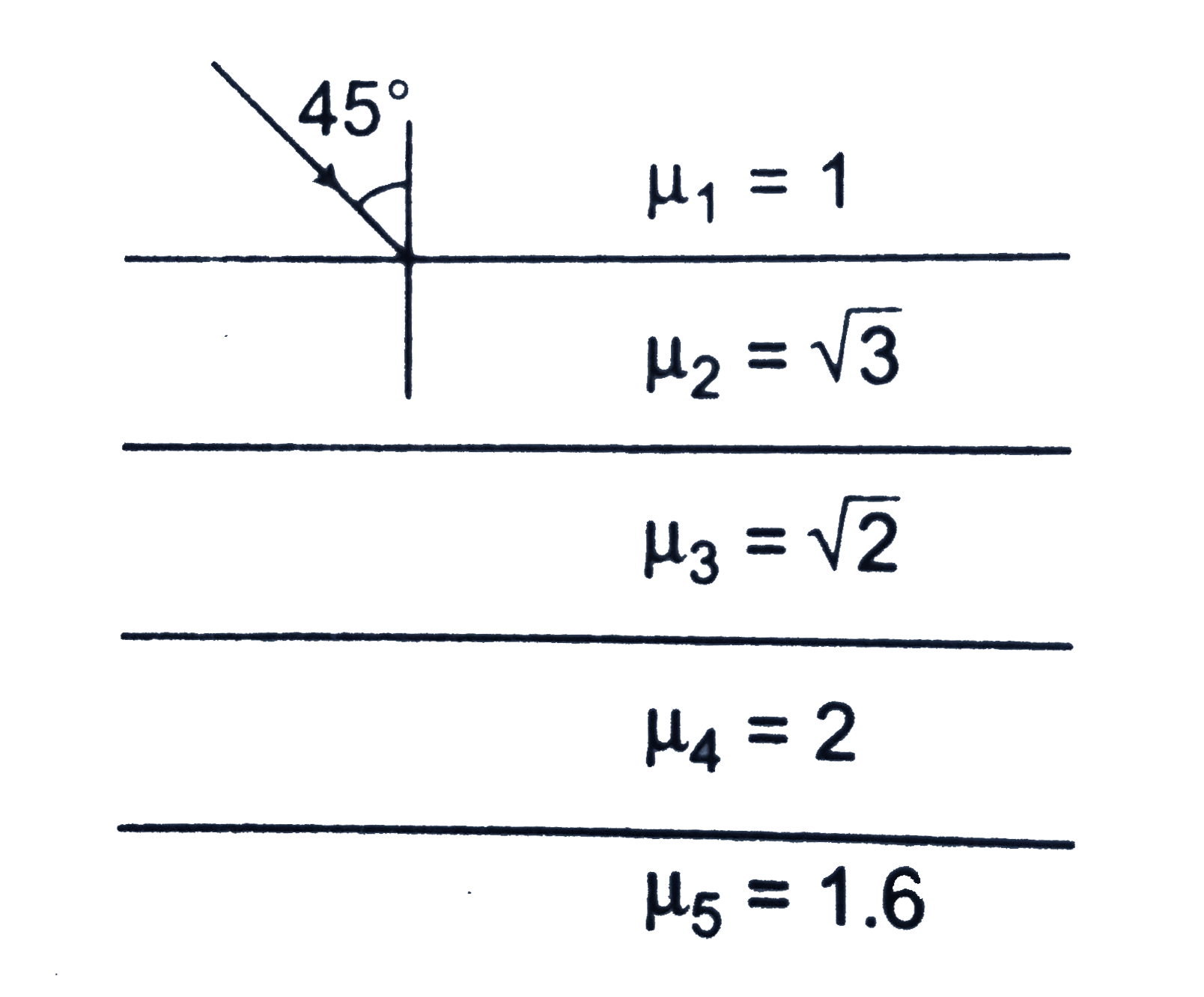
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View Solution
