$x_{1} = 3 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
Find amplitude of resultant SHM.

Video Solution

Text Solution

Verified by Experts

$x_{1} = 5 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
We can write $x_{3} = 10 sin (ω t + 270^{\circ})$
Finding the resultant amplitude by vector notation.

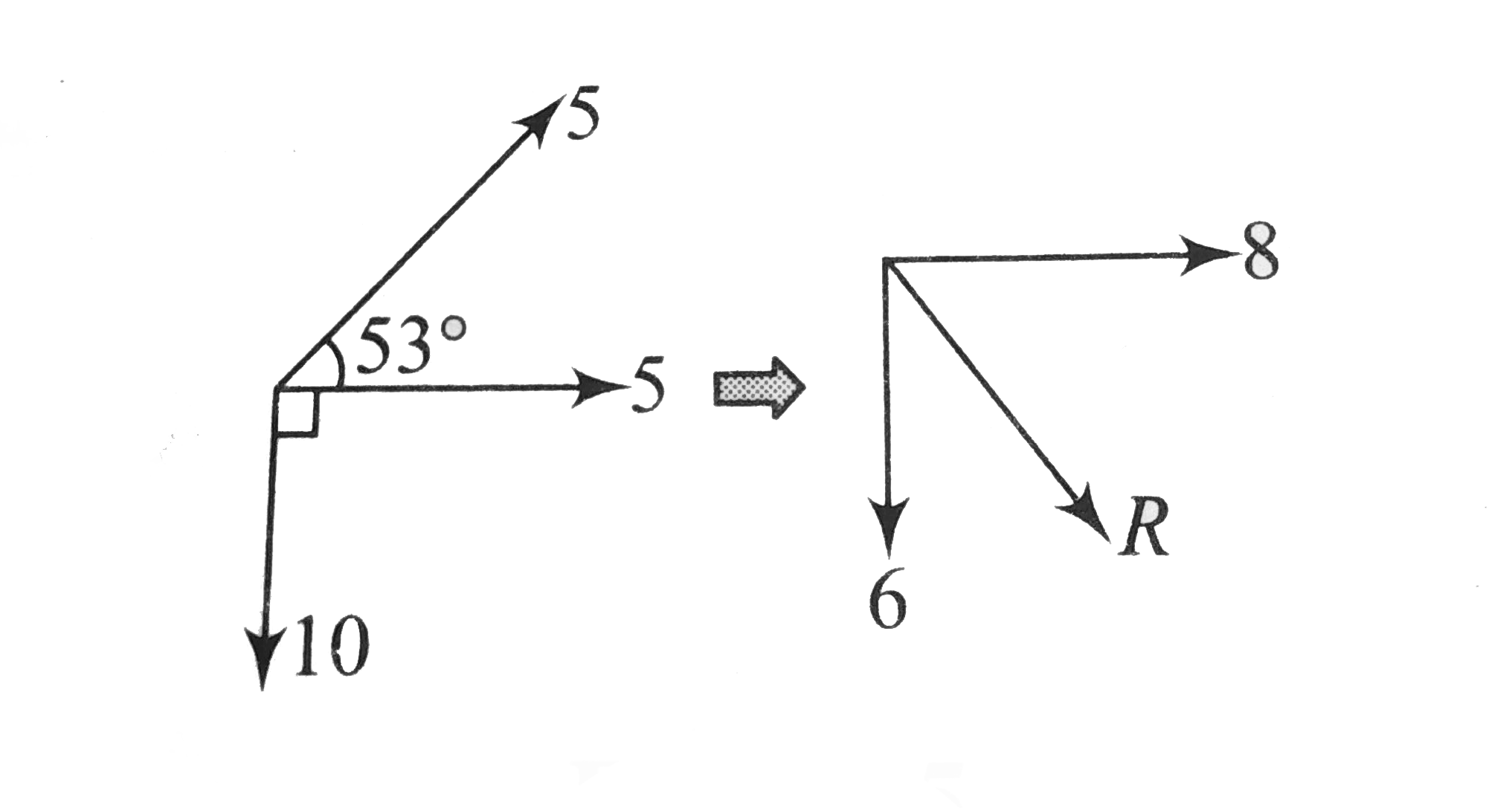
Resultant amplitude $| R | = \sqrt{8^{2} + 6^{2}} = 10$

Updated on:21/07/2023

|

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos

Similar Questions

Knowledge Check

If $i_{1} = 3 sin ω t and (i_{2}) = 4 cos ω t,$ then $(i_{3})$ is

A $5 sin (ω t + 53^{\circ})$
B $5 sin (ω t + 37^{\circ})$
C $5 sin (ω t + 45^{\circ})$
D $5 sin (ω t + 35^{\circ})$
Find the resultant amplitude of the following simple harmonic equations $:$
$x_{1} = 5 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
A5
B10
C15
D20
The resultant amplitude due to superposition of three simple harmonic motions $x_{1} = 3 sin ω t$ ,
$x_{2} = 5 sin (ω t + 37^{\circ})$ and $x_{3} = - 15 cos ω t$ is
A $18$
B $10$
C $12$
DNone of these

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Exercise 4.1

Home
Ask Doubt
Profile