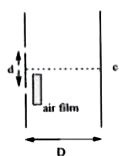
YDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000. (##DCP_V05_C32_E01_086_Q01.png" width="80%">
(1μ−1)t=mλμ
0.3t=3×0.78μm t=7.8μm.
Topper's Solved these Questions
Similar Questions
When the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View SolutionA glass sphere of refractive index 1.5 forms the real image of object O at point I as shown in the figure when kept in air of refractive index 1. If the value of x is kR. Find k
View Solution
Knowledge Check
On introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width. If μ=1.5, the thickness of the film is (wavelength of monochromatic light is λ)
A4λB3λC2λDλ
In the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.

View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionFrom the given figure, find :
x∘
View SolutionCalcium is tarnished in air , because it is covered with a thin film of
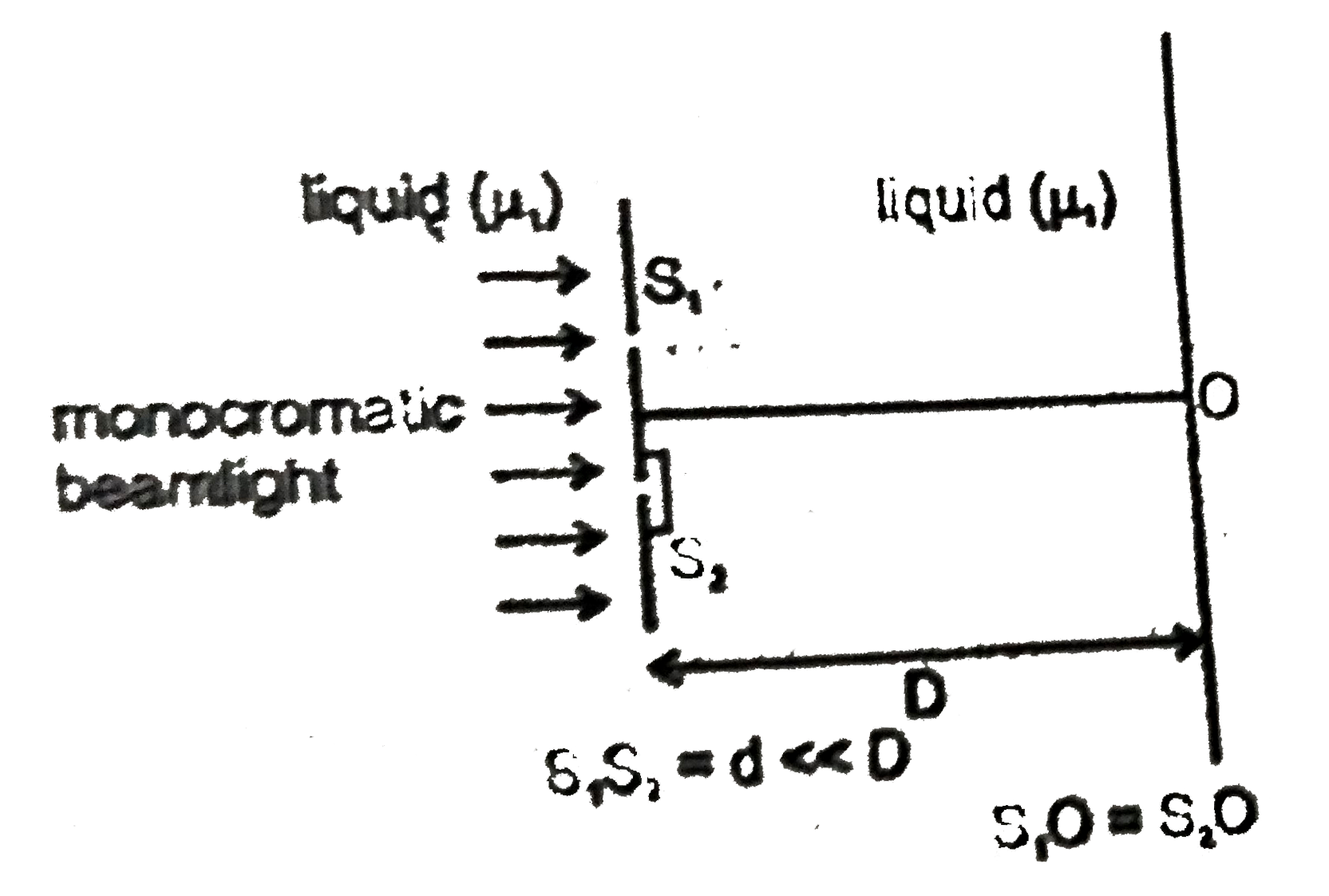
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
View Solution
