A light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
2.945×10−7m
3.945×10−7m
4.95×10−7m
1.945×10−7m
The correct Answer is:A
To find the minimum thickness of a thin air film such that it appears dark in reflected light when illuminated by light of wavelength 5890Å, we can follow these steps:
Step 1: Understand the Condition for Dark Appearance
For a thin film to appear dark in reflected light, we need to consider the interference of light waves. The condition for destructive interference (dark appearance) in a thin film is given by the formula:
2μT=(n+12)λ
where:
- μ is the refractive index of the film,
- T is the thickness of the film,
- n is an integer (0, 1, 2, ...),
- λ is the wavelength of light.
Step 2: Identify Parameters
In this case:
- The wavelength of light λ=5890Å=5890×10−10m.
- The refractive index of air μ≈1.
- For minimum thickness, we take n=0.
Step 3: Substitute Values into the Formula
Using the condition for destructive interference and substituting n=0:
2μT=(0+12)λ
This simplifies to:
2μT=12λ
Step 4: Solve for Thickness T
Now, substituting μ=1 and rearranging for T:
T=λ4μ
Substituting the values:
T=5890×10−104×1=5890×10−104
Calculating this gives:
T=5890×10−104=1472.5×10−10m=1.4725×10−7m
Step 5: Convert to Appropriate Units
To express the thickness in meters:
T=1.4725×10−7m=147.25nm
Final Answer
Thus, the minimum thickness of the film such that it appears dark in reflected light is:
1.4725×10−7m
For a thin film to appear dark in reflected light, we need to consider the interference of light waves. The condition for destructive interference (dark appearance) in a thin film is given by the formula:
2μT=(n+12)λ
where:
- μ is the refractive index of the film,
- T is the thickness of the film,
- n is an integer (0, 1, 2, ...),
- λ is the wavelength of light.
In this case:
- The wavelength of light λ=5890Å=5890×10−10m.
- The refractive index of air μ≈1.
- For minimum thickness, we take n=0.
Using the condition for destructive interference and substituting n=0:
2μT=(0+12)λ
This simplifies to:
2μT=12λ
Now, substituting μ=1 and rearranging for T:
T=λ4μ
Substituting the values:
T=5890×10−104×1=5890×10−104
Calculating this gives:
T=5890×10−104=1472.5×10−10m=1.4725×10−7m
To express the thickness in meters:
T=1.4725×10−7m=147.25nm
Thus, the minimum thickness of the film such that it appears dark in reflected light is:
1.4725×10−7m
Similar Questions
A parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
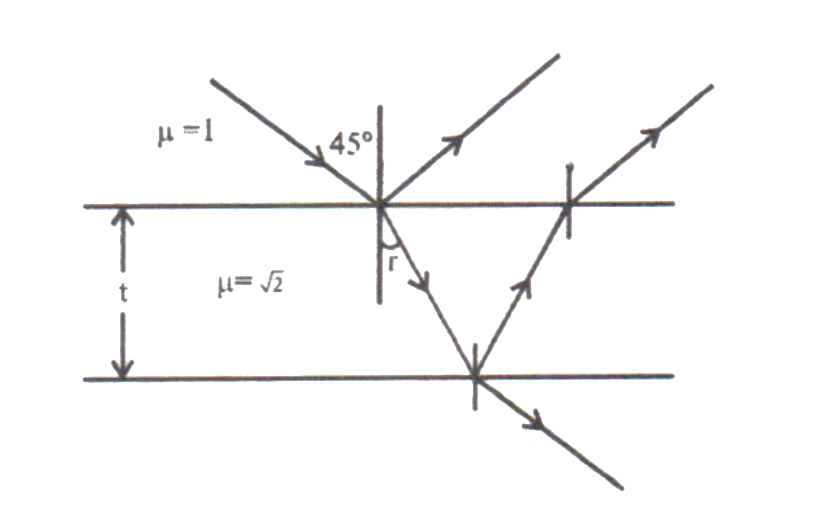
View Solution
Knowledge Check
A parallel beam of sodium light of wavelength 6000Å is incident on a thin glass plate of μ=1.5, such that the angle of refraction in the plate is 60∘. The smallest thickness of the plate which will make it appear dark by reflected light is
A3926 Ã…B4353 Ã…C1396 Ã…D1921 Ã…
Refractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionA thin oil film of refractive index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film from air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is:
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

4. If a light of wavelength λ is incident normally and the thickness of film is t, then optical path difference between waves reflected from upper and lower surface of the film is
View SolutionA certain region of a soap bubble reflects red light of vacuum wavelength λ=650nm. What is the minimum thickness that this region of the soap bubble could be have? Take the index of reflection of the soap film to be 1.41.
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View SolutionA thin oil film of refracting index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is Z×10−7m. Then find Z.
View Solution
