17s+20t=59
30s+40t=110
In the system of equations above, what is the value of t in terms of x?
2s5
s5
52s
5s
The correct Answer is:C
To solve the system of equations given by:
1. 17s+20t=59 (Equation 1)
2. 30s+40t=110 (Equation 2)
we need to find the value of t in terms of s.
Step 1: Multiply the first equation by 2
We can multiply the entire first equation by 2 to make the coefficients of t in both equations the same.
2(17s+20t)=2(59)
This simplifies to:
34s+40t=118(Equation 3)
Step 2: Subtract Equation 2 from Equation 3
Now we will subtract Equation 2 from Equation 3:
(34s+40t)−(30s+40t)=118−110
This simplifies to:
34s−30s+40t−40t=8
4s=8
Step 3: Solve for s
Now, we can solve for s:
s=84=2
Step 4: Substitute s back into Equation 1
Next, we substitute s=2 back into Equation 1 to find t:
17(2)+20t=59
This simplifies to:
34+20t=59
Step 5: Isolate t
Now, isolate t:
20t=59−34
20t=25
t=2520=54
Step 6: Express t in terms of s
Now, we want to express t in terms of s. We know s=2 and t=54.
To express t in terms of s:
t=54ands=2
We can write:
t=52s
Final Result
Thus, the value of t in terms of s is:
t=52s
2. 30s+40t=110 (Equation 2)
We can multiply the entire first equation by 2 to make the coefficients of t in both equations the same.
Now we will subtract Equation 2 from Equation 3:
Now, we can solve for s:
Next, we substitute s=2 back into Equation 1 to find t:
Now, isolate t:
Now, we want to express t in terms of s. We know s=2 and t=54.
Thus, the value of t in terms of s is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
12t+4=34t−5
In the equation above . What is the value of t?A4B9C18D36If r+s=6, what is the value of t in the equation above ?
A6B12C18D30If s=t+√r3q, what is the value of r in terms of q, s and t ?
A3√qs2−qtB3√s2−2st−t2qC3√qs2−2qst+qt2D√qs2+2qst−t23
If ts=34, what is the value of 3s4t?
View Solutiontt−3−t−22=5t−34t−12
If x and y are solutions of the equation above and y>x, what is the value of y−x?
View SolutionIntersecting lines r,s and t are shown below.
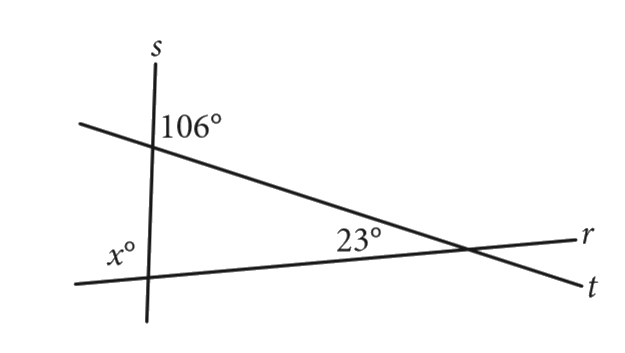
What is the value of x?
View SolutionIf 2s−3t=3t−s, what is s in terms of t?
View SolutionIf 3s+5t=10, and 2s−t=7, what is the value of 12s+3t ?
View Solution
