$A \equiv (- 4, 0), B \equiv (4, 0) \dot{M} a n d N$ are the variable points of the y-axis such that $M$ lies below $N a n d M N = 4$ . Lines $A M a n d B N$ intersect at $P \dot{}$ The locus of $P$ is $2 x y - 16 - x^{2} = 0$ $2 x y + 16 - x^{2} = 0$ $2 x y + 16 + x^{2} = 0$ $2 x y - 16 + x^{2} = 0$

A

$2 x y - 16 - x^{2} = 0$

B

$2 x y + 16 - x^{2} = 0$

C

$2 x y + 16 + x^{2} = 0$

D

$2 x y - 16 + x^{2} = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$Let M \equiv (0, h) . Then$
$or N \equiv (0, h + 4)$
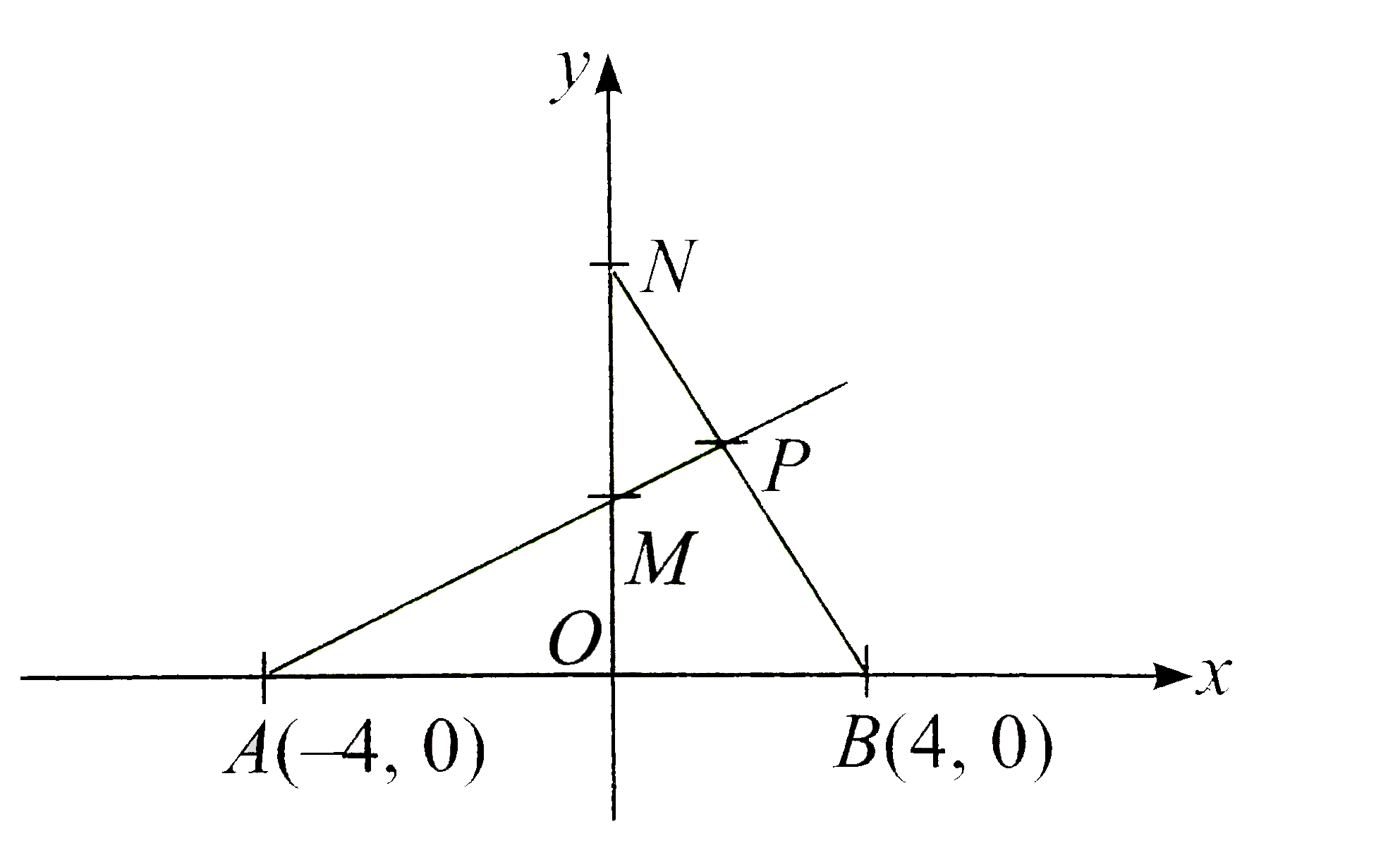
The equation of AM is
$\frac{x}{- 4} + \frac{y}{h} = 1$
$or \frac{y}{h} = \frac{4 + x}{4}$
$or h = \frac{4 y}{4 + x}$
The equation of BN is
$\frac{x}{4} + \frac{y}{h + 4} = 1$
$or \frac{y}{h + 4} = \frac{4 - x}{4}$
$or h + 4 = \frac{4 y}{4 - x}$
$or h = \frac{4 y - 16 + 4 x}{4 - x}$
$or \frac{4 (y - 4 + x)}{4 - x} = \frac{4 y}{4 + x}$ (Eliminating h)
$or 2 x y - 16 + x^{2} = 0,$ which is the required locus

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$x^{2} - 16 = 0, y^{2} - 9 y + 20 = 0$
Aif $x > y$
Bif $x \geq y$
Cif $x < y$
Dif $x \leq y$
Question 2 - Select One
Let (x,y) be any point on the parabola $y^{2} = 4 x$ . Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
A $x^{2} = y$
B $y^{2} = 2 x$
C $y^{2} = x$
D $x^{2} = 2 y$
Question 3 - Select One
The radical centre of the circles
$x^{2} + y^{2} - 16 x + 60 = 0$
$x^{2} + y^{2} - 12 x + 27 = 0$ and $x^{2} + y^{2} - 12 y + 8 = 0$ is
A $(13, \frac{33}{4})$
B $(\frac{33}{4}, - 13)$
C $(\frac{33}{4}, 13)$
DNone of these

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile