A, B and C are three points such that AB = 4 cm, BC = 3 cm and AC = 7 cm. Which one of them lies between other two ?
The correct Answer is:Point B lies between points A and C.
To determine which point lies between the other two among points A, B, and C, we can follow these steps:
1. Identify the lengths of the segments: We have the following lengths:
- AB = 4 cm
- BC = 3 cm
- AC = 7 cm
2. Use the triangle inequality: The triangle inequality states that for any three points A, B, and C, the sum of the lengths of any two sides must be greater than the length of the third side. We will check if the lengths satisfy this condition:
- Check if AB + BC > AC:
- 4 cm + 3 cm = 7 cm, which is equal to AC.
- Check if AB + AC > BC:
- 4 cm + 7 cm = 11 cm, which is greater than 3 cm.
- Check if AC + BC > AB:
- 7 cm + 3 cm = 10 cm, which is greater than 4 cm.
The first condition (AB + BC > AC) is satisfied as an equality, indicating that points A, B, and C are collinear.
3. Determine the position of the points: Since AB + BC = AC, we can conclude that point B lies between points A and C. This is because the distance from A to C (7 cm) is exactly equal to the sum of the distances from A to B (4 cm) and from B to C (3 cm).
4. Conclusion: Therefore, point B lies between points A and C.
Final Answer:
Point B lies between points A and C.
- AB = 4 cm
- BC = 3 cm
- AC = 7 cm
- Check if AB + BC > AC:
- 4 cm + 3 cm = 7 cm, which is equal to AC.
- Check if AB + AC > BC:
- 4 cm + 7 cm = 11 cm, which is greater than 3 cm.
- Check if AC + BC > AB:
- 7 cm + 3 cm = 10 cm, which is greater than 4 cm.
Point B lies between points A and C.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - SOLVED EXAMPLES21videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - NCERT SECTION (EXERCISE 5.1)7videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Olympiad/HOTS Corner13videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - WHOLE NUMBERS EXERCISE - OLYMPIAD/HOTS CORNER (FILL IN THE BLANKS)5videos
WHOLE NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
A2 cmB2.5 cmC3 cmD1.8 cm - Question 2 - Select One
ABC is a triangle in which AB = 40 cm, BC = 41 cm and AC = 9 cm. Then ortho-centre of ΔABC lies________
Ainterior of the triangleBextorior of the triangleCon the triangleDat the mid-point of the triangle - Question 3 - Select One
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 A1 cmB1.25 cmC1.5 cmDnone of these
A1 cmB1.25 cmC1.5 cmDnone of these
d(A, B) = 5cm, d(B, C) = 11 cm, d(A, C) = 6 cm which of the points is between the other two?
View SolutionIn the given figure, AC = 12 cm, AB = 3 cm and BC = 4 cm. Then cot θ = ?
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 View Solution
View SolutionIn the figure, AB=13 cm, BC=14 cm and AE =7 cm ..
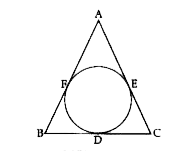
The measure of AC is :View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
View Solution

