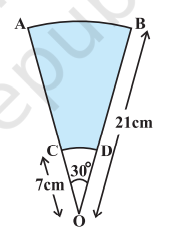
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB=30o , find the area of the shaded region.
To find the area of the shaded region between the two concentric circles, we will follow these steps:
Step 1: Calculate the area of sector OAB
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
For sector OAB:
- Radius R1=21cm
- Angle θ=30∘
Substituting the values:
Area of sector OAB=30360×π×(21)2
=112×π×441
=441π12cm2
Step 2: Calculate the area of sector ODC
Using the same formula for the area of sector ODC:
- Radius R2=7cm
Substituting the values:
Area of sector ODC=30360×π×(7)2
=112×π×49
=49π12cm2
Step 3: Find the area of the shaded region
The area of the shaded region is the area of sector OAB minus the area of sector ODC:
Area of shaded region=Area of sector OAB−Area of sector ODC
Substituting the areas calculated:
Area of shaded region=441π12−49π12
=(441−49)π12
=392π12
=98π3cm2
Step 4: Approximate the area using π≈227
To get a numerical value:
Area of shaded region≈98×2273
=215621≈102.67cm2
Thus, the area of the shaded region is approximately 102.67cm2.
---
The formula for the area of a sector is given by:
Area of sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
- Radius R1=21cm
- Angle θ=30∘
Area of sector OAB=30360×π×(21)2
=112×π×441
=441π12cm2
Using the same formula for the area of sector ODC:
- Radius R2=7cm
Area of sector ODC=30360×π×(7)2
=112×π×49
=49π12cm2
The area of the shaded region is the area of sector OAB minus the area of sector ODC:
Area of shaded region=Area of sector OAB−Area of sector ODC
Substituting the areas calculated:
Area of shaded region=441π12−49π12
=(441−49)π12
=392π12
=98π3cm2
To get a numerical value:
Area of shaded region≈98×2273
=215621≈102.67cm2
Topper's Solved these Questions
Similar Questions
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB=30o , find the area of the shaded region.
View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (See figwe). If AOB = 30°, find the area of the shaded region.

View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB=30∘, find the area of the shaded region.
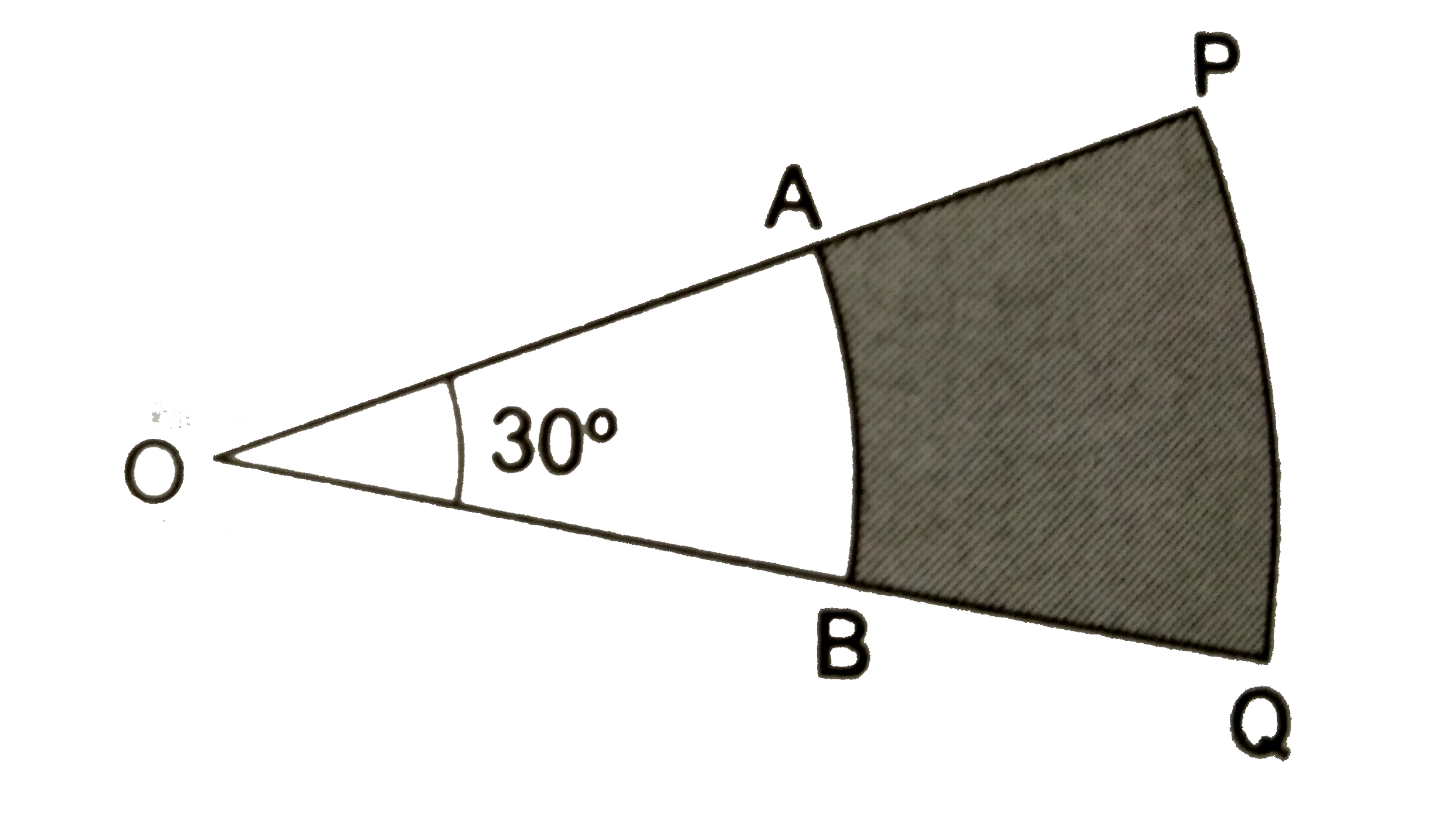
View SolutionIn the given figure PQ and AB are respectively the arcs of two concentric cicles of radii 7 cm and 3.5 cm with centre O. If ∠POQ=30∘, find the area of the shaded region.
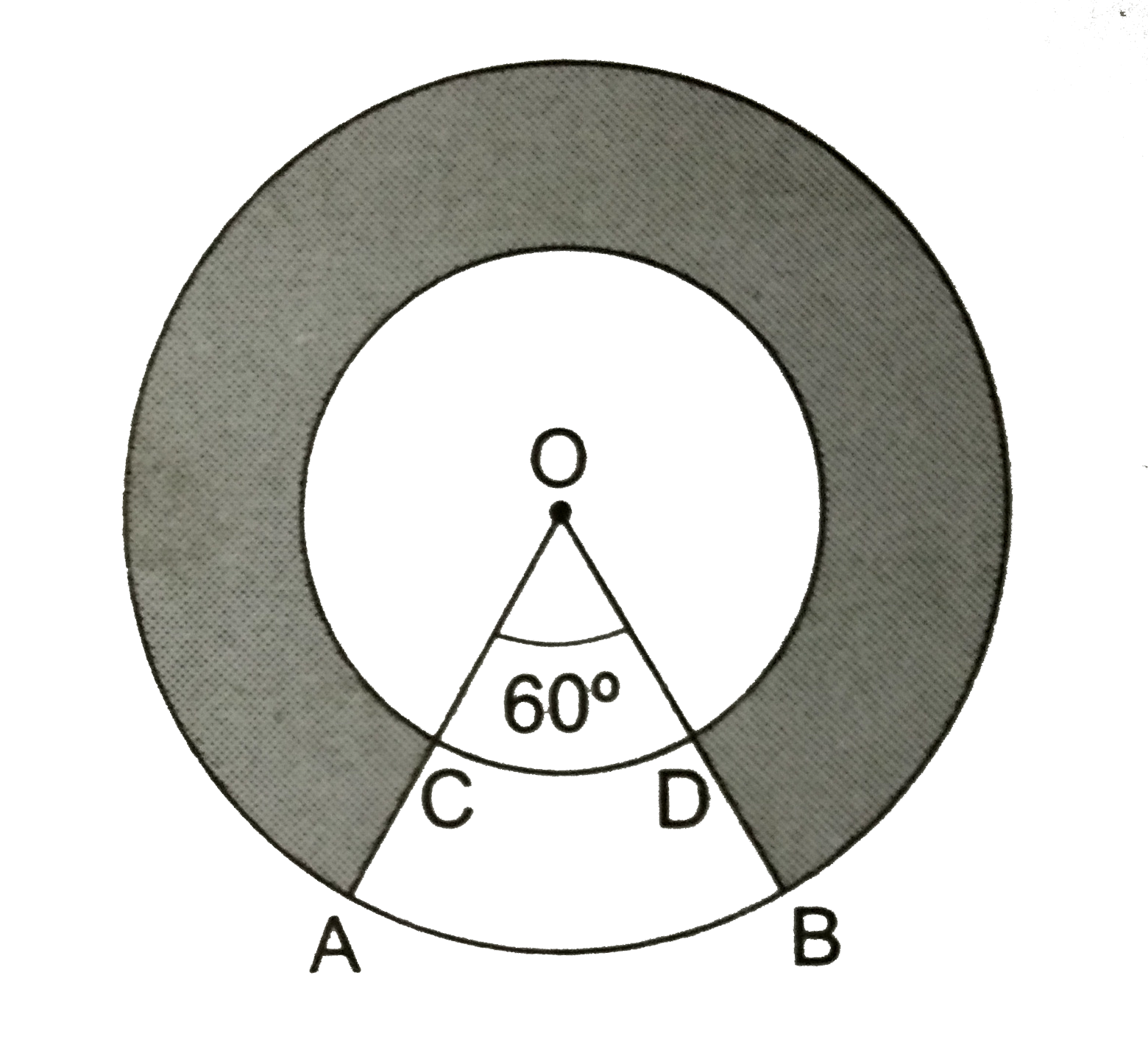
View SolutionIn the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘ find the area of the shaded region.
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.

View SolutionIn the figure, the radii of two concentric circles with centre O are 7 cm and 14 cm and ∠AOC=60∘. Find the area of the shaded region.
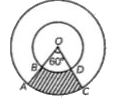
View SolutionIn the given figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB=60∘, Find the area of the shaded region

View SolutionIn Fig., two concentric circles with centre O, have radi 21cm and 42cm. If ∠AOB=60∘, find 22 the area of the shaded region. [Use π=227]
View SolutionIn Figure, there are shown sectors of two concentric circles of radii 7cm and 3.5cm. Find the area of the shaded region. (Use π=227).
View Solution
