AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB=30∘, find the area of the shaded region.
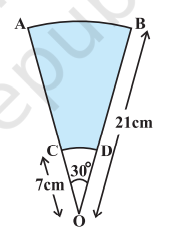
Area of the shaded region = Area of sector ABO - Area of sector CDO
Areas of sectors ABO and CDO can be found by using the formula of
Area of a sector of a circle with angle θ=θ360∘×πr2
Here, r is the radius of the circle and θ is the degree measure if the angle
For both the sectors ABO and CDO angle, θ=30∘ and radii is 21 cm and 7 cm respectively.
Radius of the sector ABO, R = OB = 21 cm
Radius of the sector CDO, r = OD = 7 cm
Area of shaded region = Area of sector ABO - Area of sector CDO
= θ360∘×πR2−θ360∘×πr2
= θ360∘×π(R2−r2)= 30∘360∘×227[(21cm)2−(7cm)2]
= 112×227×(441cm2−49cm2)
= 1142×392cm2
= 3083cm2
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBook:NCERTChapter:AREAS RELATED TO CIRCLESExercise:EXERCISE 12.1
Explore 5 Videos
- AREAS RELATED TO CIRCLESBook:NCERTChapter:AREAS RELATED TO CIRCLESExercise:SOLVED EXAMPLES
Explore 6 Videos
- AREAS RELATED TO CIRCLESBook:NCERTChapter:AREAS RELATED TO CIRCLESExercise:SOLVED EXAMPLES
Explore 6 Videos
- ARITHMETIC PROGRESSIONSBook:NCERTChapter:ARITHMETIC PROGRESSIONSExercise:Exercise 5.3
Explore 20 Videos
Similar Questions
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB=30∘, find the area of the shaded region.

View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (See figwe). If AOB = 30°, find the area of the shaded region.

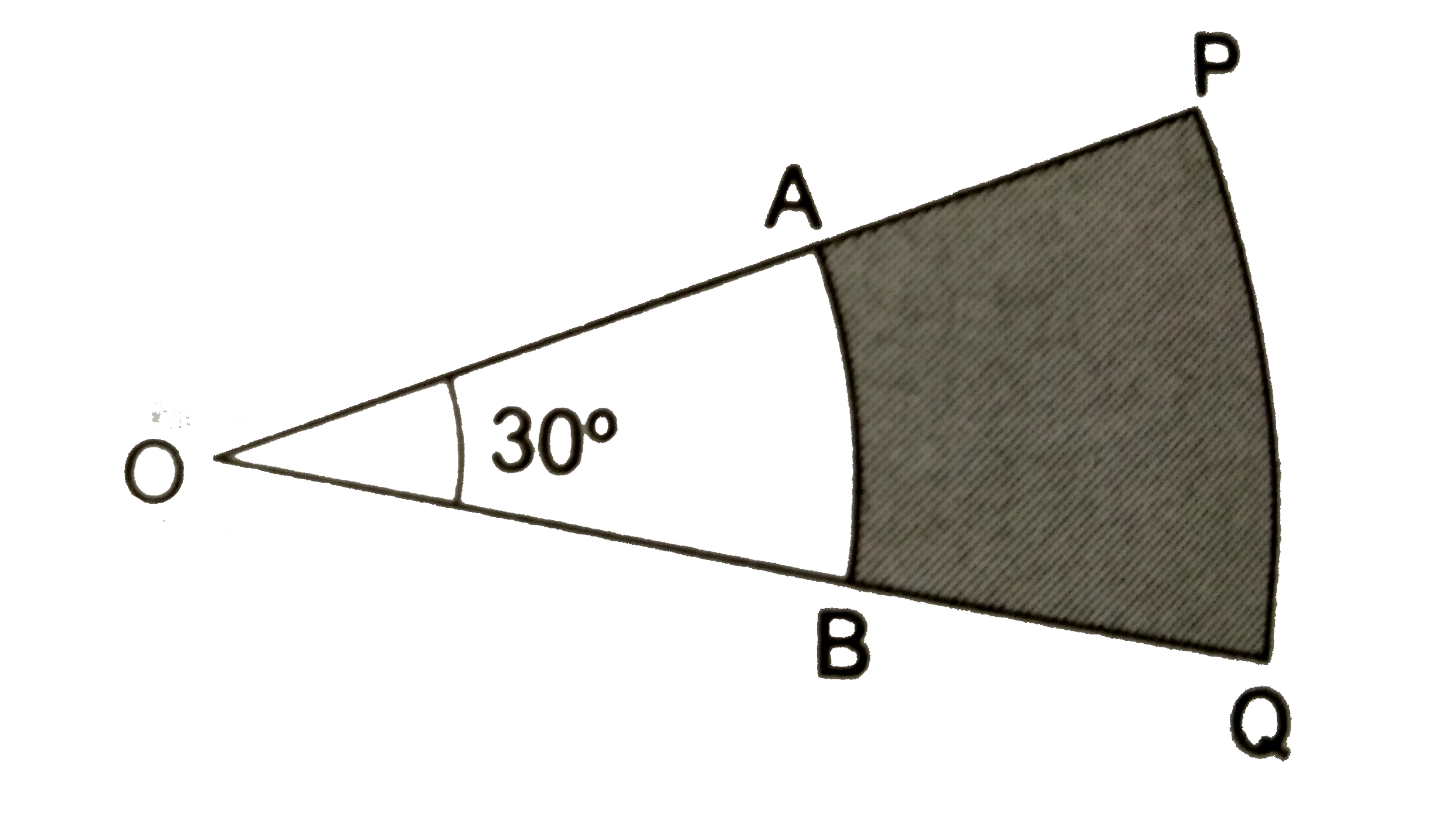
View SolutionIn the given figure PQ and AB are respectively the arcs of two concentric cicles of radii 7 cm and 3.5 cm with centre O. If ∠POQ=30∘, find the area of the shaded region.
View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB=30o , find the area of the shaded region.
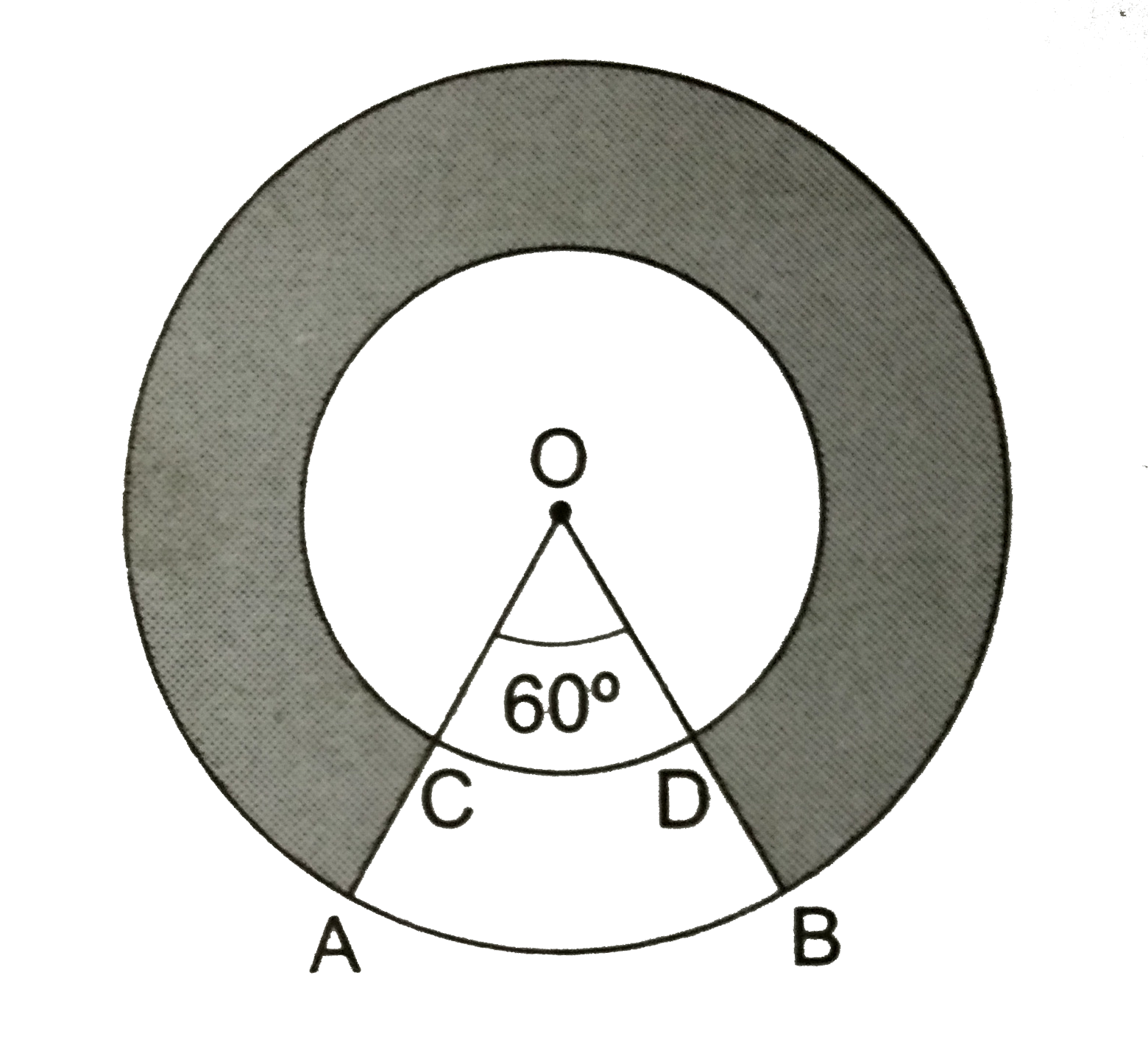
View SolutionIn the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘ find the area of the shaded region.
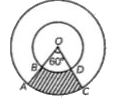
View SolutionIn the figure, the radii of two concentric circles with centre O are 7 cm and 14 cm and ∠AOC=60∘. Find the area of the shaded region.
View SolutionIn the given figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB=60∘, Find the area of the shaded region

View SolutionIn Fig., two concentric circles with centre O, have radi 21cm and 42cm. If ∠AOB=60∘, find 22 the area of the shaded region. [Use π=227]
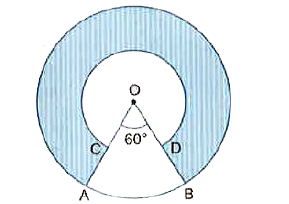
View SolutionIn the adjoining figure, two concentric circle with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘, find the area of the shaded region. (Use π=227)

View SolutionIn figure, OACB is a quadrant of a circle with centre O and radius 7 cm. If AD = 2 cm, find the area of the shaded region.

View Solution