AB, CD, and EF are three concurrent lines passing through the point O such that OF bisects ∠BOD. If ∠BOF=350, find ∠BOC and ∠AOD.
To solve the problem step by step, we will follow the reasoning presented in the video transcript.
1. Identify the Given Information:
- We have three concurrent lines: AB, CD, and EF, all intersecting at point O.
- The line OF bisects angle BOD.
- Angle BOF = 35 degrees.
2. Determine Angle BOD:
- Since OF bisects angle BOD, we can say:
∠BOD=∠BOF+∠DOF
- Given that angle BOF = 35 degrees, and since OF bisects BOD, we have:
∠DOF=∠BOF=35 degrees
- Therefore:
∠BOD=35+35=70 degrees
3. Use the Straight Line Property:
- On line AOB, we know that:
∠AOD+∠BOD=180 degrees
- Substituting the value of angle BOD:
∠AOD+70=180
- Solving for angle AOD:
∠AOD=180−70=110 degrees
4. Determine Angle BOC:
- Since lines AOB and FOE intersect at point O, angle AOD and angle BOC are vertically opposite angles. Therefore:
∠BOC=∠AOD=110 degrees
Final Answers:
- ∠BOC=110 degrees
- ∠AOD=110 degrees
- We have three concurrent lines: AB, CD, and EF, all intersecting at point O.
- The line OF bisects angle BOD.
- Angle BOF = 35 degrees.
- Since OF bisects angle BOD, we can say:
∠BOD=∠BOF+∠DOF
- Given that angle BOF = 35 degrees, and since OF bisects BOD, we have:
∠DOF=∠BOF=35 degrees
- Therefore:
∠BOD=35+35=70 degrees
- On line AOB, we know that:
∠AOD+∠BOD=180 degrees
- Substituting the value of angle BOD:
∠AOD+70=180
- Solving for angle AOD:
∠AOD=180−70=110 degrees
- Since lines AOB and FOE intersect at point O, angle AOD and angle BOC are vertically opposite angles. Therefore:
∠BOC=∠AOD=110 degrees
- ∠BOC=110 degrees
- ∠AOD=110 degrees
Topper's Solved these Questions
Similar Questions
In Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View SolutionIn Fig.25, find ∠x. Further find ∠BOC, ∠COD and ∠AOD.
View SolutionIn Figure, lines AB and CD intersect at O. If ∠AOC+ ∠BOE=700and ∠BOD=400, find ∠BOE and reflex ∠COE
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=440, find ∠OAD
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionIn Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
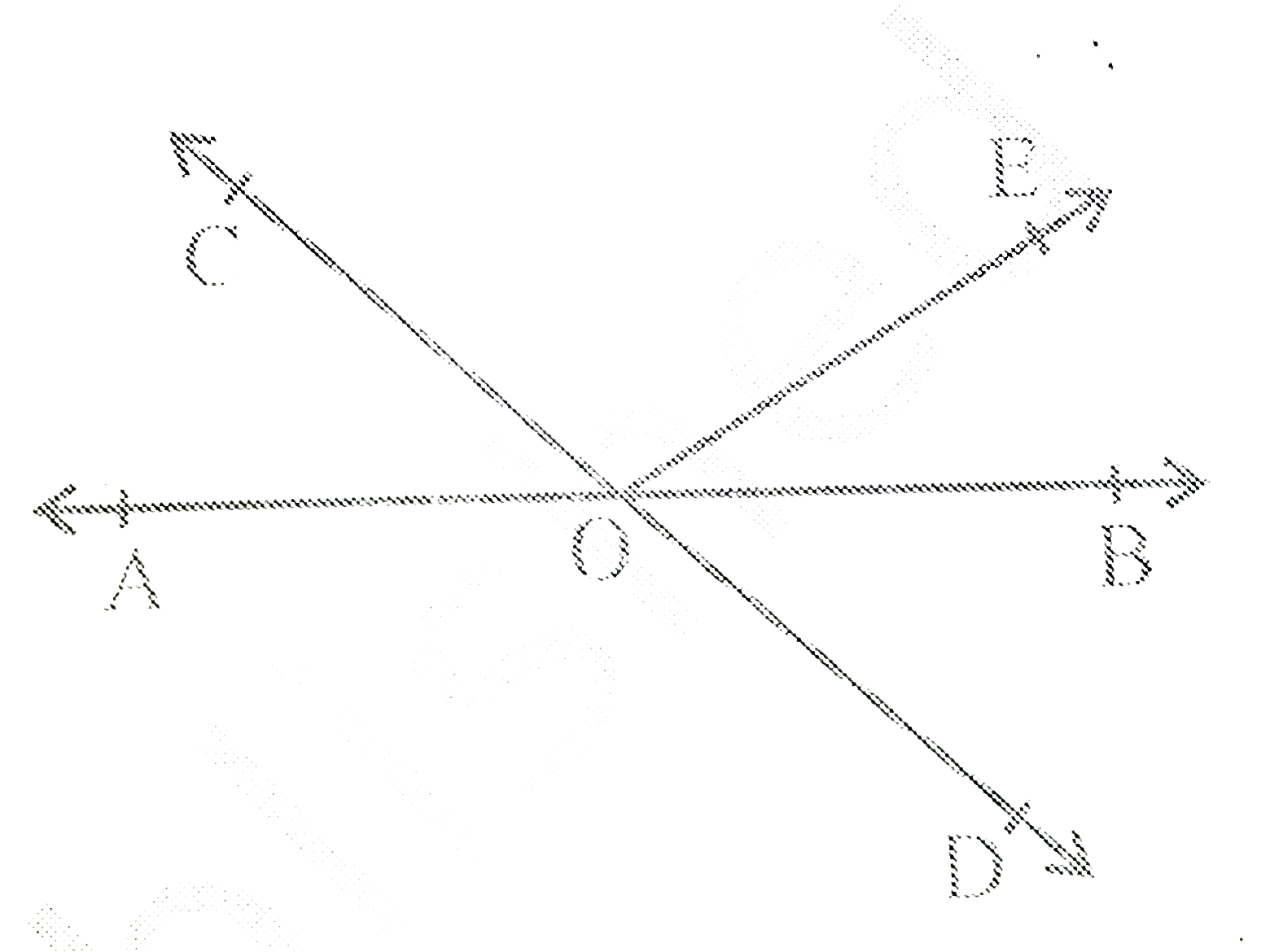 View Solution
View SolutionIn Fig. 8, ∠AOC and ∠BOC form a linear pair. Determine the value of x.
View SolutionIn Fig. ∠AOC and ∠BOC form a linear pair. Determine the value of x
View Solution

